复数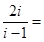 ( )
( )
A.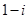 |
B.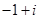 |
C. |
D.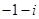 |
已知 是非空集合,命题甲:
是非空集合,命题甲: ,命题乙:
,命题乙: ,那么( )
,那么( )
| A.甲是乙的充分不必要条件 |
| B.甲是乙的必要不充分条件 |
| C.甲是乙的充要条件 |
| D.甲是乙的既不充分也不必要条件 |
已知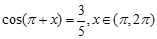 ,则
,则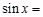 ( )
( )
A.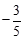 |
B. |
C.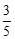 |
D.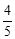 |
等差数列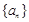 中,已知
中,已知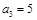 ,
,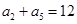 ,
,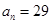 ,则
,则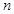 为( )
为( )
| A.13 | B.14 | C.15 | D.16 |
在△ABC中,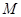 是
是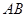 边所在直线上任意一点,若
边所在直线上任意一点,若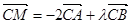 ,则
,则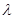 =( )
=( )
| A.1 | B.2 | C.3 | D.4 |
已知函数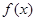 是定义在R上的增函数,则函数
是定义在R上的增函数,则函数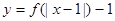 的图象可能是( )
的图象可能是( )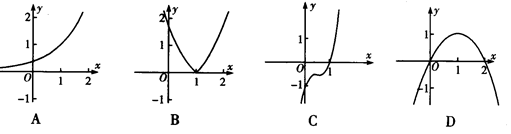
在200m高的山顶上,测得山下一塔顶与塔底的俯角分别是30°、60°,则塔高为( )
A.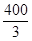 m m |
B.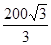 m m |
C.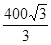 m m |
D.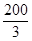 m m |
已知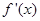 是定义在R上的函数
是定义在R上的函数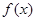 的导函数,且
的导函数,且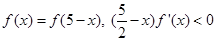 若
若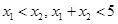 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.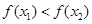 |
B.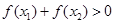 |
C.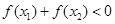 |
D.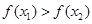 |
设 ,若
,若 是
是 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )
| A.[-1,2] | B.[-1,0] | C.[1,2] | D.[0,2] |
在△ABC中,已知 ,P为线段AB上的点,且
,P为线段AB上的点,且 的最大值为( )
的最大值为( )
| A.3 | B.4 | C.5 | D.6 |
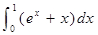 等于 .
等于 .
函数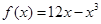 在区间
在区间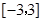 上的最小值是 .
上的最小值是 .
数列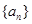 中,已知
中,已知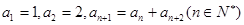 ,则
,则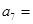 ________.
________.
方程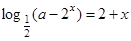 有解,则
有解,则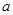 的最小值为_________
的最小值为_________
下列命题中,真命题有_______(写出所有真命题的序号)
(1)在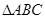 中,“
中,“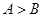 ”是“
”是“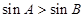 ”的充要条件;
”的充要条件;
(2)点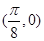 为函数
为函数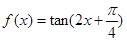 的一个对称中心;
的一个对称中心;
(3)若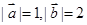 ,向量
,向量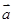 与向量
与向量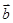 的夹角为
的夹角为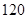 °,则
°,则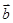 在向量
在向量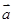 上的投影为
上的投影为 ;
;
(4)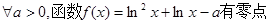 .
.
已知函数 (
(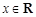 ),
),
(1)求函数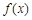 的最小值;
的最小值;
(2)已知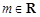 ,
,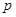 :关于
:关于 的不等式
的不等式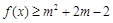 对任意
对任意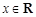 恒成立;
恒成立;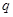 :函数
:函数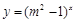 是增函数.若“
是增函数.若“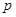 或
或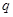 ”为真,“
”为真,“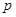 且
且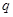 ”为假,求实数
”为假,求实数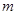 的取值范围.
的取值范围.
设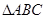 的内角
的内角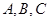 所对的边分别为
所对的边分别为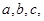 且
且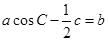 .
.
(1)求角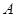 的大小;
的大小;
(2)若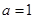 ,求
,求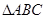 的周长的取值范围.
的周长的取值范围.
(本小题满分12分)已知数列 的前
的前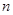 项和为
项和为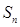 ,且有
,且有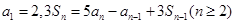 .
.
(1)求数列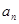 的通项公式;
的通项公式;
(2)若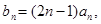 求数列
求数列 的前n项和
的前n项和
(本小题满分13分)直三棱柱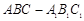 中,
中,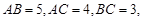
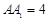 ,点
,点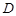 在
在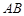 上.
上.
(Ⅰ)若 是
是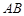 中点,求证:
中点,求证: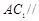 平面
平面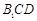 ;
;
(Ⅱ)当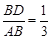 时,求二面角
时,求二面角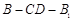 的余弦值.
的余弦值.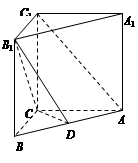
(本小题13分)为了保护环境,某工厂在政府部门的鼓励下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(Ⅰ)当 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
(Ⅱ)当处理量为多少吨时,每吨的平均处理成本最少?
(本小题满分13分)设函数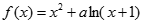 有两个极值点
有两个极值点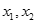 ,且
,且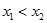 .
.
(1)求实数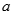 的取值范围;
的取值范围;
(2)讨论函数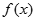 的单调性;
的单调性;
(3)若对任意的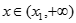 ,都有
,都有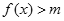 成立,求实数
成立,求实数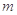 的取值范围.
的取值范围.