集合 的子集个数为 .
的子集个数为 .
“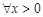 ,
,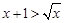 ”的否定是 .
”的否定是 .
函数 的最大值是 .
的最大值是 .
已知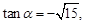 且
且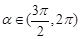 ,则
,则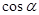 = .
= .
等差数列 中,
中,
 则该数列前十项的和
则该数列前十项的和 .
.
平面向量
 ,
,
 ,则
,则 与
与 的夹角为 .
的夹角为 .
已知 ,若
,若 ,则
,则 .
.
如图,在 中,已知
中,已知 ,
, 是
是 边上一点,
边上一点, ,
, ,
, ,则
,则 .
.
已知直线 与
与 在点
在点 处的切线互相垂直,则
处的切线互相垂直,则 .
.
函数 的零点个数是 .
的零点个数是 .
已知平行四边形 中,
中, ,
, ,则平行四边形
,则平行四边形 的面积为 .
的面积为 .
已知正实数 满足
满足 ,则
,则 的最小值为 .
的最小值为 .
已知函数 ,若存在两个不相等的实数
,若存在两个不相等的实数 ,使得
,使得 ,则
,则 的取值范围为 .
的取值范围为 .
若关于x的不等式ax2+x-2a<0的解集中仅有4个整数解,则实数a的取值范围为 .
已知向量
 ,
,
 ,
,

 .
.
(1)求函数 的单调递减区间及其图象的对称轴方程;
的单调递减区间及其图象的对称轴方程;
(2)当 时,若
时,若 ,求
,求 的值.
的值.
已知△ 的面积为
的面积为 ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求△ABC的面积
,求△ABC的面积 .
.
如图,已知海岛 到海岸公路
到海岸公路 的距离
的距离 为
为 ,
, ,
, 间的距离为
间的距离为 ,从
,从 到
到 ,必须先坐船到
,必须先坐船到 上的某一点
上的某一点 ,船速为
,船速为 ,再乘汽车到
,再乘汽车到 ,车速为
,车速为 ,记
,记 .
.
(1)试将由 到
到 所用的时间
所用的时间 表示为
表示为 的函数
的函数 ;
;
(2)问 为多少时,由
为多少时,由 到
到 所用的时间
所用的时间 最少?
最少?
已知函数 ,
, ,
, .
.
(1) ,
, ,求
,求 值域;
值域;
(2) ,解关于
,解关于 的不等式
的不等式

 .
.
设函数 .
.
(1) ,
, ,求
,求 的单调增区间;
的单调增区间;
(2) ,
, ,若
,若

 对一切
对一切 恒成立,求
恒成立,求 的最小值
的最小值 的表达式;
的表达式;
已知等差数列 ,其前
,其前 项和为
项和为 .若
.若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对任意
 ,将数列
,将数列 中落入区间
中落入区间 内的项的个数记为
内的项的个数记为 ;
;
①求数列 的通项公式
的通项公式 ;
;
②记 ,数列
,数列 的前
的前 项和为
项和为 ,求所有使得等式
,求所有使得等式 成立的正整数
成立的正整数 ,
, .
.
(几何证明选讲)(本小题满分10分)如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB·CD = BC·DE.
(矩阵与变换)(本小题满分10分)已知曲线 ,在矩阵M
,在矩阵M 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,
, 在矩阵N
在矩阵N 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,求曲线
,求曲线 的方程.
的方程.
(极坐标与参数方程)(本小题满分10分) 已知曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 ,判断两曲线的位置关系.
,判断两曲线的位置关系.
(不等式选讲)(本小题满分10分)已知a,b是正实数,求证: .
.
(本小题满分10分)在如图所示的多面体中,四边形 为正方形,四边形
为正方形,四边形 是直角梯形,
是直角梯形, ,
, 平面
平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.
(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去 班听课的概率;
班听课的概率;
(2)设随机变量 为这五名评估员去
为这五名评估员去 班听课的人数,求
班听课的人数,求 的分布列和数学期望.
的分布列和数学期望.