0的相反数是 ，-2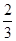
的倒数是 。
在数轴上，与表示-3的点的距离为5个单位长度的点表示的数有 个，它是 。
地球上的海洋面积约为36100000千米2，用科学记数法表示为 千米2。
若｜a+2｜+（b-1）2=0，则（a+b）2015= 。
绝对值不大于4的整数有 。
若a2+3b=2，则代数式2a2+6b-8=
若单项式
与
的和仍为单项式，则其和为 。
如果多项式
与多项式
相等，那么
某服装厂生产生一批服装，每天生产a件，计划b天完成，为提前投放市场，需提前5天，用代数式表示该厂实际每天比原计划多生产 件。
用围棋子按下面的规律摆图形，则摆第n个图形需要围棋子的枚数是 （用含n的代数式表示）
若有理数x的相反数是8，则x为（ ）
| A．-8 | B．8 | C．- |
D． |
若｜a｜=5，则a是（ ）
| A．5 | B．-5 | C．±5 | D． |
如果ab＜0，那么下列说法正确的是（ ）
| A．a＜0，b＜0 |
| B．a＜0，b＞0 |
| C．a＞0，b＜0 |
| D．a＜0，b＞0或a＞0，b＜0 |
在数轴上，0为原点，某点A移动到B，移动了12.6个单位长度；点A表示数a，点B表示数b，且a+b=0，A到0的距离为（ ）
| A．12.6 | B．6.3 | C．-12.6 | D．-6.3 |
下列各组数中，相等的一组是（ ）
A． 与-32 |
B．｜-3｜2与-32 |
C． 与-33 |
D．｜-3｜3与-33 |
已知0＜a＜1，则a，-a，-
，的大小关系为（ ）
| A．＞-＞-a＞a |
B．-＞a＞-a＞ |
| C．＞a＞-＞-a |
D．＞a＞-a＞- |
若A、B都是6次多项式，则A+B是（ ）
A、6次多项式
B、12次多项式
C、次数不超过6次的多项式
D、次数不低于6次的多项式
若a＞0，ab＜0，则｜b-a-1｜-|a-b+3|的值为（ ）
| A．2 | B．-2 | C．-2a+2b+4 | D．2a-2b-4 |
若a、b互为相反数，c、d互为倒数，｜m｜=2，则代数式m2-3cd+
的值为（ ）
| A．-1 | B．1 | C．-7 | D．1或-7 |
某校礼堂第一排有35个座位，往后每一排多2个座位，则第n排的座位用含n的代数式表示为（ ）
| A．35+2n | B．35+n | C．34+n | D．33+2n |
计算（4分×4=16分）
（1）
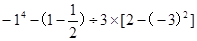
（2）
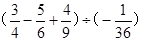
（3）
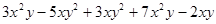
（4）
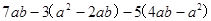
先化简，再求值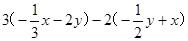
，其中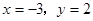
如果x2-x+1的2倍减去一个多项式得到3x2+4x-1，求这个多项式.
若有理数x、y满足｜x｜=7，｜y｜=4，且｜x+y｜=x+y，求x-y的值
已知a、b两数在数轴上表示如图
（1）试在数轴上找出表示-a，-b的点，并用“＜”连接a，b，-a，-b
（2）化简：｜a-b｜-｜b｜+｜a｜
如图，正方形的边长为a，用整式表示图中阴影部分的面积，并计算当a=2时阴影部分的面积（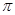
取3.14）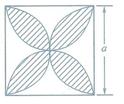
若“△”表示一种新运算，规定a△b=a×b-（a+b），请计算下列各式的值
（1）-3△5 （2）2△[（-4）△（-5）]
某地电话拨号上网有两种收费方式，用户可以任选一种。
A、计时制，每分钟0.05元；
B、包月制：每月50元（限一部个人住宅电话上网）。
此外，每种上网方式都要增收每分钟0.02元的通讯费
（1）某用户某月上网时间为x小时，请用代数式表示两种收费方式下，该用户分别应支付的费用。
A: B:
（2）若某用户估计每月上网时间为20小时，通过计算说明应该采用哪一种付费方式较为合算。