已知f（x）=（2x+1）3﹣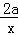
+3a，若f′（﹣1）=8，则f（﹣1）=（ ）
| A．4 | B．5 | C．﹣2 | D．﹣3 |
若f（x）=2lnx﹣x2，则f′（x）＞0的解集为（ ）
| A．（0，1） |
| B．（﹣∞，﹣1）∪（0，1） |
| C．（﹣1，0）∪（1，+∞） |
| D．（1，+∞） |
函数y=xsin2x的导数是（ ）
| A．y′=sin2x﹣xcos2x | B．y′=sin2x﹣2xcos2x |
| C．y′=sin2x+xcos2x | D．y′=sin2x+2xcos2x |
函数f（x）=ax3+bx2+cx+d（a≠0），若a+b+c=0，导函数f′（x）满足f′（0）f′（1）＞0，设f′（x）=0的两根为x1，x2，则|x1﹣x2|的取值范围是（ ）
A． |
B． |
C． |
D． |
若函数f（x）在R上可导，且满足f（x）＞xf′（x），则（ ）
| A．3f（1）＞f（3） | B．3f（1）＜f（3） | C．3f（1）=f（3） | D．f（1）=f（3） |
已知函数f（x）=sinx+lnx，则f′（1）的值为（ ）
| A．1﹣cos1 | B．1+cos1 | C．cos1﹣1 | D．﹣1﹣cos1 |
函数f（x）=
ex（sinx+cosx）在区间[0，
]上的值域为（ ）
A．[ ，e] |
B．（，e） |
C．[1，e] |
D．（1，e） |
函数
的导数是（ ）
A． |
B．﹣sinx | C． |
D． |
设y=﹣2exsinx，则y′等于（ ）
| A．﹣2excosx | B．﹣2exsinx | C．2exsinx | D．﹣2ex（sinx+cosx） |
已知函数f（x）=ax3+3x2+2，若f′（﹣1）=4，则a的值是（ ）
A． |
B． |
C． |
D． |
设函数f（x）的导数f′（x），且f（x）=f′（
）cosx+sinx，则f′（
）=（ ）
| A．1 | B．0 | C． |
D． |
函数
的导数是（ ）
A． |
B． |
C．ex﹣e﹣x | D．ex+e﹣x |
函数y=x2﹣2x在﹣2处的导数是（ ）
| A．﹣2 | B．﹣4 | C．﹣6 | D．﹣8 |
若
，则y′=（ ）
A． |
B． |
C． |
D． |
函数f（x）=ex+xsinx﹣7x在x=0处的导数等于（ ）
| A．﹣4 | B．﹣5 | C．﹣6 | D．﹣7 |
下列结论正确的是（ ）
A．若y=x+ ，则y′=1+ |
| B．若y=cosx，则y′=sinx |
C．若y= ，则y′= |
D．若y= ，则y′= |
函数f（x）=xsinx+cosx的导数是（ ）
| A．xcosx+sinx | B．xcosx | C．xcosx﹣sinx | D．cosx﹣sinx |
的导数是（ ）
A． |
B． |
C． |
D． |
已知函数f（x）=xex，f′（x）是f（x）的导函数，则f′（0）等于（ ）
| A．﹣2 | B．﹣1 | C．0 | D．1 |
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3﹣3x2，则可求得
=（ ）
| A．4025 | B．﹣4025 | C．8050 | D．﹣8050 |