已知集合
，
，则集合
（ ）
A． |
B． |
C． |
D． |
下列函数中，与函数
的奇偶性相同，且在
上单调性也相同的是 （ ）
A． |
B． |
C． |
D． |
已知平面
，
是
内不同于
的直线，那么下列命题中错误的是 （ ）
A．若 ，则 |
B．若，则 |
C．若 ，则 |
D．若，则 |
已知
，
，
，
，则向量
在向量
上的投影为 （ ）
A． |
B． |
C． |
D． |
若“
”是“
”的必要不充分条件，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
在等差数列
中
，且
，则
的最大值等于（ ）
| A．3 | B．6 | C．9 | D．36 |
已知圆
的弦过点
，当弦长最短时，该弦所在直线方程为 （ ）
A． |
B． |
C． |
D． |
若将函数
的图象向右平移
个单位，得到的图象关于y轴对称，则
的最小值是（ ）
| A． |
B． |
C． |
D． |
抛物线
的焦点为
,点
为该抛物线上的动点,又点
,则
的最小值是 （ ）
A． |
B． |
C． |
D． |
已知点
，点
在曲线
上，若线段
与曲线
相交且交点恰
为线段的中点，则称点为曲线
与曲线
的一个“相关点”，记曲线与曲线的“相关点”的
个数为
，则（ ）
A． |
B． |
C． |
D． |
定义在R上的奇函数
，当
时，
，则不等式
的解集
是_____________.
已知
，且
，则
=____.
一个几何体的三视图如图所示，则此几何体的体积为________.
已知变量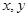
满足约束条件
，则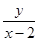
的取值范围为__________________.
已知等差数列
的前
项和为
，
，若对于任意的
自然数，都有
，则
=________________.
在矩形ABCD中，
,P为矩形内一点，且
，若
，则
的最大值为_______.
已知抛物线
的准线与双曲线
交于
、
两点，点
为抛物线的焦点，若
为直角三角形，则双曲线离心率的取值范围是 ．
设函数
（Ⅰ）求
的最小正周期及值域；
（Ⅱ）已知
中，角
的对边分别为
，若
，
，
，求的面积．
已知函数
，其中
（Ⅰ）求函数
的定义域；
（Ⅱ）若对任意
恒有
，试确定
的取值范围．
如图，
是等腰直角三角形，
，
，
分别为
的中点，沿
将
折起，得到如图所示的四棱锥
．
（Ⅰ）在棱
上找一点
，使
∥平面
；
（Ⅱ）当四棱锥的体积取最大值时，求平面与平面
夹角的余弦值．
数列
首项
，前
项和
与
之间满足
．
（Ⅰ）求证：数列
是等差数列；
（Ⅱ）求数列的通项公式；
（Ⅲ）设存在正数
，使
对
都成立，求的最大值．
已知椭圆
经过点
，其离心率为
，经过点
，斜率为
的直线
与椭圆
相交于
两点．
（Ⅰ）求椭圆的方程；
（Ⅱ）求的取值范围；
（Ⅲ）设椭圆与
轴正半轴、
轴正半轴分别相交于
两点，则是否存在常数，使得向量
与
共线？如果存在，求值；如果不存在，请说明理由．