若向量 ,且
,且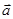 与
与 的夹角余弦为
的夹角余弦为 ,则
,则 等于( )
等于( )
A.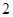 |
B.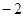 |
C.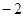 或 或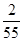 |
D.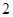 或 或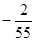 |
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )
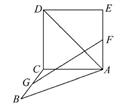
A. |
B. |
C. |
D. |
已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于( ).
A.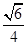 |
B.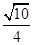 |
C.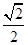 |
D. |
若A ,B
,B ,C
,C ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.不等边锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.等边三角形 |
若A ,B
,B ,当
,当 取最小值时,
取最小值时, 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
空间四边形 中,
中, ,
, ,则
,则 <
< >的值是( )
>的值是( )
A. |
B. |
C.- |
D. |
已知正方体 的棱长是
的棱长是 ,则直线
,则直线 与
与 间的距离为 .
间的距离为 .
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF= ,则下列结论中错误的是
,则下列结论中错误的是

①AC⊥BE
②EF∥平面ABCD
③三棱锥ABEF的体积为定值
④异面直线AE,BF所成的角为定值
如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,则点B到平面EFG的距离是

已知正方体ABCD- 的棱长为1,求直线
的棱长为1,求直线 与AC的距离.
与AC的距离.
如图,四棱锥 的底面
的底面 为菱形,
为菱形, ,侧面
,侧面 是边长为2的正三角形,侧面
是边长为2的正三角形,侧面
 底面
底面 .
.
(Ⅰ)设 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(Ⅱ)求斜线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在侧棱 上存在一点
上存在一点 ,使得二面角
,使得二面角 的大小为
的大小为 ,求
,求 的值.
的值.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1存在点D,使得AD⊥A1B,并求 的值.
的值.