已知函数y＝x3－3x＋c的图象与x轴恰有两个公共点，则c＝（ ）
| A．－2或2 | B．－9或3 | C．－1或1 | D．－3或1 |
已知f（x）＝x3－ax在[1，＋∞）上是单调增函数，则a的最大值是（ ）
| A．0 | B．1 | C．2 | D．3 |
设
，若函数
，
有大于零的极值点，则
A． |
B． |
C． |
D． |
已知函数f（x）＝ax3－3x2＋1，若f（x）存在唯一的零点x0，且x0>0，则a的取值范围是（ ）
| A．（2，＋∞） | B．（1，＋∞） |
| C．（－∞，－2） | D．（－∞，－1） |
已知y＝f（x）是奇函数，当x∈（0,2）时，f（x）＝ln x－ax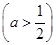
，当x∈（－2,0）时，f（x）的最小值为1，则a的值等于（ ）
A． |
B． |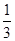
C． |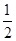
D．1 |
当x∈[－2，1]时，不等式ax3－x2＋4x＋3≥0恒成立，则实数a的取值范围是（ ）
| A．[－5，－3] | B． |
| C．[－6，－2] | D．[－4，－3] |
若函数f（x）＝x3－3x＋a有三个不同的零点，则实数a的取值范围为________．
球的直径为d，其内接正四棱柱体积V最大时的高为（ ）
A． d |
B． d |
C． d |
D． d |
（能力提高）已知函数f（x）＝x3＋ax2＋bx＋c有两个极值点x1，x2．若f（x1）＝x1<x2，则关于x的方程3（f（x））2＋2af（x）＋b＝0的不同实根个数为（ ）
| A．3 | B．4 | C．5 | D．6 |
函数
（
）．若存在
，使
，求a的取值范围．
已知函数f（x）＝
（k为常数，e＝2．718 28…是自然对数的底数），曲线y＝f（x）在点（1，f（1））处的切线与x轴平行．
（1）求k的值；
（2）求f（x）的单调区间；
（3）（能力提升）设g（x）＝xf′（x），其中f′（x）为f（x）的导函数．证明：对任意x>0，g（x）<1＋e－2．
（高考真题）已知函数
，其中
，
为自然对数的底数。
（1）设
是函数
的导函数，求函数在区间
上的最小值；
（2）（能力提升）若
，函数在区间
内有零点，求
的取值范围