已知集合 ,
, ,那么集合
,那么集合 是( )
是( )
A. |
B. |
C. |
D. |
设 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则 =( )
=( )
| A.11 | B.5 | C.-8 | D.-11 |
函数 ,
, ( )
( )
| A.是偶函数 | B.是奇函数 | C.不具有奇偶性 | D.奇偶性与 有关 有关 |
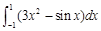 等于( )
等于( )
| A.0 | B.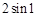 |
C.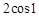 |
D.2 |
若函数 ,则此函数图像在点(1,f(1))处的切线的倾斜角为( )
,则此函数图像在点(1,f(1))处的切线的倾斜角为( )
| A.直角 | B.0 | C.锐角 | D.钝角 |
下列命题正确的个数有( )
(1)命题“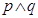 为真”是命题“
为真”是命题“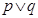 为真”的必要不充分条件
为真”的必要不充分条件
(2)命题“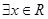 ,使得
,使得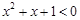 ”的否定是:“对
”的否定是:“对 , 均有
, 均有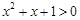 ”
”
(3)经过两个不同的点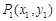 、
、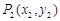 的直线都可以用方程
的直线都可以用方程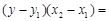
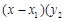
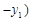 来表示
来表示
(4)在数列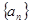 中,
中, 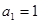 ,
,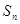 是其前
是其前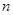 项和,且满足
项和,且满足 ,则
,则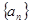 是等比数列
是等比数列
(5)若函数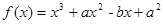 在
在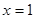 处有极值10,则
处有极值10,则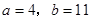
| A.1个 | B.2个 | C.3个 | D.4个 |
某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )
A. |
B. |
C. |
D. |
直角三角形的斜边长为 ,则其内切圆半径的最大值为( )
,则其内切圆半径的最大值为( )
A. |
B. |
C. |
D. |
在平面直角坐标系 中,设点
中,设点 为圆
为圆 :
: 上的任意一点,点
上的任意一点,点
 ,其中
,其中 ,则线段
,则线段 长度的最小值为( )
长度的最小值为( )
A. |
B. |
C. |
D. |
 是同一球面上的四个点,其中
是同一球面上的四个点,其中 是正三角形,
是正三角形,  ⊥平面
⊥平面 ,
, ,
, ,则该球的表面积为( )
,则该球的表面积为( )
A. |
B. |
C. |
D. |
已知定义在 上的函数
上的函数 满足①
满足① ,②
,② ,③在
,③在 上表达式为
上表达式为 ,则函数
,则函数 与函数
与函数 的图像在区间
的图像在区间 上的交点个数为( )
上的交点个数为( )
| A.5 | B.6 | C.7 | D.8 |
设等差数列 满足:
满足: ,公差
,公差 ,若当且仅当
,若当且仅当 时,数列
时,数列 的前
的前 项和
项和 取得最大值,则首项
取得最大值,则首项 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 ,
, 为单位向量,当向量
为单位向量,当向量 的夹角为
的夹角为 时,
时, 在
在 上的投影为 .
上的投影为 .
已知点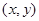 满足不等式组
满足不等式组 ,其中
,其中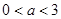 ,则
,则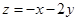 的最小值为__________.
的最小值为__________.
已知 ,函数
,函数 在
在 上单调递减,则
上单调递减,则 ________.
________.
定义函数 ,若存在常数
,若存在常数 ,对于任意
,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在
在 上的“均值”为
上的“均值”为 ,已知
,已知 ,则函数
,则函数 在
在 上的“均值”为________.
上的“均值”为________.
(本小题满分12分)已知 分别是
分别是 的三个内角
的三个内角 的对边,
的对边, .
.
(1)求角 的大小;
的大小;
(2)若 的面积
的面积 ,求
,求 周长的最小值.
周长的最小值.
(本小题满分12分)设公差不为0的等差数列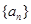 的首项为1,且
的首项为1,且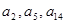 构成等比数列.
构成等比数列.
(1)求数列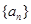 的通项公式;
的通项公式;
(2)设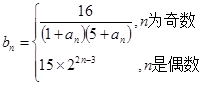 ,求数列
,求数列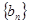 的前
的前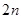 项和
项和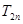 .
.
(本小题满分12分)如图,四棱锥中, ∥,,侧面为等
边三角形. 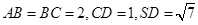 .
. 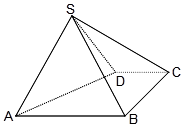
(1)证明: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知椭圆C: 短轴的两个顶点与右焦点的连线构成等边三角形,直线
短轴的两个顶点与右焦点的连线构成等边三角形,直线 与以椭圆C的上顶点为圆心,以椭圆C的长半轴长为半径的圆相切.
与以椭圆C的上顶点为圆心,以椭圆C的长半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)椭圆C与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与椭圆C交于
分别与椭圆C交于 ,
, 两点,
两点,  分别为直线
分别为直线 、
、 的斜率,
的斜率,  ,求证:直线
,求证:直线 过定点,并求出该定点坐标;
过定点,并求出该定点坐标;
(3)在(2)的条件下,求 面积的最大值.
面积的最大值.
(本小题满分12分)设函数 ,
, ,(
,( 是自然对数的底数).
是自然对数的底数).
(1)讨论 在其定义域上的单调性;
在其定义域上的单调性;
(2)若 ,且不等式
,且不等式 对于
对于 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分10分)设函数 .
.
(1)求函数 的最小值;
的最小值;
(2)若 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.