设集合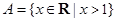 ,
,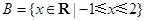 ,则
,则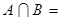 ( )
( )
A.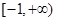 |
B.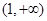 |
C.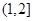 |
D.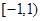 |
已知向量 ,
, . 若
. 若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若等比数列 满足
满足 ,且公比
,且公比 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向左平移 个单位 个单位 |
B.向左平移 个单位 个单位 |
C.向右平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
设 ,
, ,
, ,则( )
,则( )
A. |
B. |
C. |
D. |
设 ,则“
,则“ 且
且 ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
已知函数 若关于
若关于 的方程
的方程 有三个不相等的实数根,则实数
有三个不相等的实数根,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设等差数列 的前
的前 项和为
项和为 .在同一个坐标系中,
.在同一个坐标系中, 及
及 的部分图象如图所示,则( )
的部分图象如图所示,则( )
A.当 时, 时, 取得最大值 取得最大值 |
B.当 时, 时, 取得最大值 取得最大值 |
C.当 时, 时, 取得最小值 取得最小值 |
D.当 时, 时, 取得最小值 取得最小值 |
设复数 ,则
,则 ______.
______.
已知函数 的图象关于
的图象关于 轴对称,则实数
轴对称,则实数 的值是 .
的值是 .
 ________.
________.
为净化水质,向一个游泳池加入某种化学药品,加药后池水中该药品的浓度 (单位:
(单位: )随时间
)随时间 (单位:
(单位: )的变化关系为
)的变化关系为 ,则经过_______
,则经过_______ 后池水中药品的浓度达到最大.
后池水中药品的浓度达到最大.
如图所示,在△ABC中, 为
为 边上的一点, 且
边上的一点, 且 .若
.若 ,则
,则 .
.
已知函数 (
( 是常数,
是常数, )的最小正周期为
)的最小正周期为 ,设集合
,设集合 {直线
{直线 为曲线
为曲线 在点
在点 处的切线,
处的切线, }.若集合
}.若集合 中有且只有两条直线互相垂直,则
中有且只有两条直线互相垂直,则 = ;
= ; = .
= .
(本小题满分13分)已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的单调递增区间.
的单调递增区间.
(本小题满分13分)已知 是各项均为正数的等比数列,
是各项均为正数的等比数列, ,且
,且 成等差数列.
成等差数列.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(本小题满分13分)如图所示,在四边形 中,
中, ,且
,且 .
.
(Ⅰ)求△ 的面积;
的面积;
(Ⅱ)若 ,求
,求 的长.
的长.
(本小题满分14分)已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)若 ,求函数
,求函数 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)若 在区间
在区间 上恒成立,求
上恒成立,求 的最大值.
的最大值.
(本小题满分13分)已知数列 的前
的前 项和
项和 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: ;
;
(Ⅲ)判断数列 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分14分)设函数 ,
, 为曲线
为曲线 在点
在点 处的切线.
处的切线.
(Ⅰ)求L的方程;
(Ⅱ)当 时,证明:除切点
时,证明:除切点 之外,曲线C在直线L的下方;
之外,曲线C在直线L的下方;
(Ⅲ)设 ,且满足
,且满足 ,求
,求 的最大值.
的最大值.