下列图形中,是轴对称图形的为 ( )
A、 B、 C、 D、
下列实数 ,
, ,
,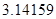 ,
,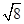 ,
, ,
, 中无理数有( )
中无理数有( )
A.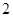 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
下列点中,位于直角坐标系第二象限的点是( )
| A.(2,1) | B.(-2,-1) | C.(-2,1) | D.(2,-1) |
下列运算正确的是( )
A. |
B. |
C. |
D. |
下列命题正确的个数有:(1) ;(2)
;(2) ;(3)无限小数都是无理数;(4)有限小数都是有理数;(5)实数分为正实数和负实数两类 ( )
;(3)无限小数都是无理数;(4)有限小数都是有理数;(5)实数分为正实数和负实数两类 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
由四舍五入法得到的近似数为8.01×10-4精确到( ).
| A.万位 | B.百分位 | C.百万分位 | D.百位 |
若xy>0,则点(x,y)在直角坐标系中位于( ).
| A.x轴上 | B.y轴上 | C.第一或第三象限 | D.第二或第四象限 |
如果点M在直线 上,则M点的坐标可以是( )
上,则M点的坐标可以是( )
| A.(-1,0) | B.(0,1) | C.(1,0) | D.(1,-1) |
等腰三角形的一个角是100°,其底角是 °
 的平方根是 。
的平方根是 。
点P(-3,-4)到原点的距离为________。
在直角坐标系中,点A(2,1)向左平移4个单位再向下平移2个单位后的坐标为_________。
点A(-2,3)关于y轴对称点的坐标是 。
如果一个正数的两个平方根是 和
和 ,则这个数为
,则这个数为
已知 的整数部分为a,小数部分为b,则a-b= 。
的整数部分为a,小数部分为b,则a-b= 。
在直角坐标系中,y轴上与A(1,0)的距离等于2的点的坐标是 。
要使y=(m-2) 是关于x的一次函数,则m=______________。
是关于x的一次函数,则m=______________。
将自然数按以下规律排列:
第一列 第二列 第三列 第四列 第五列
第一行 1 4 5 16 17
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 …
表中数2在第二行,第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应,根据这一规律,数2014对应的有序数对为 .
计算:(1) (
( -
- )
)
(2)| | + |
| + | | +
| + 
解方程:(1)x2-36=0
(2)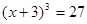
已知y与x+2成正比例,且x=1时,y=-6,求y与x之间的函数关系式.
在如图的方格纸中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)建立直角坐标系,使点B的坐标为(-5,2),点C的坐标为(-2,2),则点A的坐标为 ;
(2)画出 绕点P顺时针旋转
绕点P顺时针旋转 后的△A1B1C1并写出点A1的坐标为 。
后的△A1B1C1并写出点A1的坐标为 。
如图,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积。
如图,A(—1,0),C(1,4),点B在x轴上,且AB=3。
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积。
如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.
小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L。油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示。根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.