若 表示
表示 ,求
,求 的值。
的值。
定义新运算为a△b=(a+1)÷b,求值:6△(3△4).
设 △
△ ,那么,5△
,那么,5△ ______,(5△2) △
______,(5△2) △ _____.
_____.
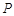 、
、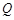 表示数,
表示数,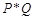 表示
表示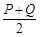 ,求3
,求3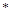 (6
(6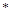 8) .
8) .
已知a,b是任意自然数,我们规定: a⊕b= a+b-1, ,那么
,那么 .
.
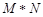 表示
表示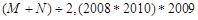
 .
.
“△”是一种新运算,规定:a△b=a×c+b×d(其中c,d为常数),如5△7=5×c+7×d。如果1△2=5,2△3=8,那么6△1OOO的计算结果是________。
对于非零自然数a和b,规定符号 的含义是:a
的含义是:a b=
b=
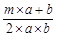 (m是一个确定的整数)。如果1
(m是一个确定的整数)。如果1 4=2
4=2 3,那么3
3,那么3 4等于________。
4等于________。
对于任意的整数x与y定义新运算“△”: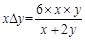 ,求2△9。
,求2△9。
“*”表示一种运算符号,它的含义是: ,已知
,已知 ,求
,求 。
。
[A]表示自然数A的约数的个数.例如4有1,2,4三个约数,可以表示成[4]=3.计算: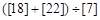 = 。
= 。
x为正数,<x>表示不超过x的质数的个数,如<5.1>=3,即不超过5.1的质数有2,3,5共3个.那么<<19>+<93>+<4>×<1>×<8>>的值是 .
定义运算“△”如下:对于两个自然数a和b,它们的最大公约数与最小公倍数的和记为a△b.例如:4△6=(4,6)+[4,6]=2+12=14.根据上面定义的运算,18△12= .
我们规定:符号 表示选择两数中较大数的运算,例如:5
表示选择两数中较大数的运算,例如:5 3=3
3=3 5=5,符号△表示选择两数中较小数的运算,例如:5△3=3△5=3,计算:
5=5,符号△表示选择两数中较小数的运算,例如:5△3=3△5=3,计算: 的结果是多少?
的结果是多少?
规定:符号“&”为选择两数中较大数的运算,“◎”为选择两数中较小数的运算。计算下式:[(7◎3)& 5]×[ 5◎(3 & 7)] = .
如果规定a※b =13×a-b ÷8,那么17※24的最后结果是______.
若用G(a)表示自然数a的约数的个数,如:自然数6的约数有1、2、3、6,共4个,记作G(6)=4,则G(36)+G(42)= .
如果 ,那么
,那么 。
。
“华”、“杯”、“赛”三个字的四角号码分别是“2440”、“4199”和“3088”,将“华杯赛”的编码取为244041993088,如果这个编码从左起的奇数位的数码不变,偶数位的数码改变为关于9的补码,例如:0变9,1变8等,那么“华杯赛”新的编码是________.
羊和狼在一起时,狼要吃掉羊.所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼,以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。小朋友总是希望羊能战胜狼.所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼,这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算.运算的结果或是羊,或是狼.求下式的结果:羊△(狼☆羊)☆羊△(狼△狼) = 。
一般我们都认为手枪指向谁,谁好像是有危险的,下面的规则同学们能看懂吗?
规定:警察 小偷
小偷 警察,警察
警察,警察 小偷
小偷 小偷.
小偷.
那么:(猎人 小兔)
小兔) (山羊
(山羊 白菜)
白菜) .
.
如果a△b表示 ,例如3△4
,例如3△4 ,那么,当a△5=30时, a= .
,那么,当a△5=30时, a= .
规定新运算※:a※b=3a-2b.若x※(4※1)=7,则x= .
如果a⊙b表示 ,例如4⊙5=3×4-2×5=2,那么,当x⊙5比5⊙x大5时, x= .
,例如4⊙5=3×4-2×5=2,那么,当x⊙5比5⊙x大5时, x= .
对于数a、b、c、d,规定,< a、b、c、d >=2ab-c+d,已知< 1、3、5、x >=7,求x的值。
定义新运算为 ,⑴求
,⑴求 的值;⑵若
的值;⑵若 则x的值为多少?
则x的值为多少?
对于任意的两个自然数 和
和 ,规定新运算
,规定新运算 :
: ,其中
,其中 、
、 表示自然数.如果
表示自然数.如果 ,那么
,那么 等于几?
等于几?
定义 为
为 与
与 之间(包含
之间(包含 、
、 )所有与
)所有与 奇偶性相同的自然数的平均数,例如:
奇偶性相同的自然数的平均数,例如: ,
, .在算术
.在算术 的方格中填入恰当的自然数后可使等式成立,那么所填的数是多少?
的方格中填入恰当的自然数后可使等式成立,那么所填的数是多少?
如有 #
# 新运算,
新运算, #
# 表示
表示 、
、 中较大的数除以较小数后的余数.例如;2#7=1,8#3=2,9#16=7,21#2=1.如(21#(21#
中较大的数除以较小数后的余数.例如;2#7=1,8#3=2,9#16=7,21#2=1.如(21#(21# ))=5,则
))=5,则 可以是________(
可以是________( 小于50)
小于50)
已知 、
、 满足
满足 ,
, ;其中
;其中 表示不大于
表示不大于 的最大整数,
的最大整数, 表示
表示 的小数部分,即
的小数部分,即 ,那么
,那么 。
。
规定:A○B表示A、B中较大的数,A△B表示A、B中较小的数.若(A○5+B△3)×(B○5+ A△3)=96,且A、B均为大于0的自然数,A×B的所有取值为 .
如果1※2=1+11
2※3=2+22+222
3※4=3+33+333+333+3333
计算 (3※2)×5。
规定:6※2=6+66=72
2※3=2+22+222=246,
1※4=1+11+111+1111=1234.
7※5= .
有一个数学运算符号 ,使下列算式成立:
,使下列算式成立:  ,
, ,
, ,
, ,求
,求
规定 △
△
 , 计算:(2△1)
, 计算:(2△1) (11△10)
(11△10) ______.
______.
一个数n的数字中为奇数的那些数字的和记为 ,为偶数的那些数字的和记为
,为偶数的那些数字的和记为 ,例如
,例如 ,
, .
. ;
; = .
= .
已知:10△3=14, 8△7=2,  △
△ ,根据这几个算式找规律,如果
,根据这几个算式找规律,如果  △
△ =1,那么
=1,那么 = .
= .
如果 、
、 、
、 是3个整数,则它们满足加法交换律和结合律,即
是3个整数,则它们满足加法交换律和结合律,即
⑴a+b=b+a;⑵ 。
。
现在规定一种运算"*",它对于整数a、 b、c 、d 满足:
(a,b)*(c,d)=(a×c+b×d,a×c-b×d)。
例:
请你举例说明,"*"运算是否满足交换律、结合律。
在计算机中,对于图中的数据(或运算)的读法规则是:先读第一分支圆圈中的,再读与它相连的第二分支左边的圆圈中的,最后读与它相连的第二分支右边的圆圈中的,也就是说,对于每一个圆圈中的数据(或运算)都是按"中→左→右"的顺序。如:图A表示:2+3, B表示2+3×2-1。图C中表示的式子的运算结果是________ 。
对于任意有理数x, y,定义一种运算“※”,规定:x※y= ,其中的
,其中的 表示已知数,等式右边是通常的加、减、乘运算.又知道1※2=3,2※3=4,x※m=x(m≠0),则m的数值是 _________.
表示已知数,等式右边是通常的加、减、乘运算.又知道1※2=3,2※3=4,x※m=x(m≠0),则m的数值是 _________.
x、y表示两个数,规定新运算“*”及“△”如下:x*y=mx+ny,x△y=kxy,其中 m、n、k均为自然数,已知 1*2=5,(2*3)△4=64,求(1△2)*3的值.
对于任意的两个自然数 和
和 ,规定新运算
,规定新运算 :
: 


 ,其中
,其中 、
、 表示自然数.⑴求1
表示自然数.⑴求1 100的值;⑵已知
100的值;⑵已知
 10
10 75,求
75,求 为多少?⑶如果(
为多少?⑶如果( 3)
3) 2
2 121,那么
121,那么 等于几?
等于几?
两个不等的自然数a和b,较大的数除以较小的数,余数记为a☉b,比如5☉2=1,7☉25=4,6☉8="2." (8级)
(1)求1991☉2000,(5☉19)☉19,(19☉5)☉5;
(2)已知11☉x=2,而x小于20,求x;
(3)已知(19☉x)☉19=5,而x小于50,求x.
设a,b是两个非零的数,定义a※b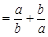 .
.
(1)计算(2※3)※4与2※(3※4).
(2)如果已知a是一个自然数,且a※3=2,试求出a的值.
定义运算“⊙”如下:
对于两个自然数a和b,它们的最大公约数与最小公倍数的差记为a⊙b.
比如:10和14,最小公倍数为70,最大公约数为2,则10⊙14=70-2=68.
(1)求12⊙21,5⊙15;
(2)说明,如果c整除a和b,则c也整除a⊙b;如果c整除a和a⊙b,则c也整除b;
(3)已知6⊙x=27,求x的值.
“⊙”表示一种新的运算符号,已知:2⊙3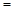
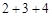 ;7⊙2
;7⊙2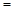
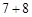 :3⊙5
:3⊙5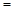
 ,……按此规则,如果n⊙8
,……按此规则,如果n⊙8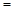 68,那么,n
68,那么,n 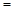 ____.
____.
国际统一书号ISBN由10个数字组成,前面9个数字分成3组,分别用来表示区域、出版社和书名,最后一个数字则作为核检之用。核检码可以根据前9个数字按照一定的顺序算得。如:某书的书号是ISBN 7-107-17543-2,它的核检码的计算顺序是:
①7×10+1×9+0×8+7×7+1×6+7×5+5×4+4×3+3×2=207;
②207÷11=18……9;
③11-9=2。这里的2就是该书号的核检码。
依照上面的顺序,求书号ISBN-7-303-07618-□的核检码。
如图一只甲虫从画有方格的木板上的A点出发,沿着一段一段的横线、竖线爬行到B,图1中的路线对应下面的算式: .请在下面右图中用粗线画出对应于算式:
.请在下面右图中用粗线画出对应于算式: 的路线.
的路线. 