设集合 ,则满足
,则满足 的集合
的集合 的个数是( )
的个数是( )
| A.1 | B.3 | C.4 | D.8 |
 ( )
( )
A. |
B. |
C. |
D.18 |
下列函数中周期为 且为偶函数的是( )
且为偶函数的是( )
A. |
B. |
C. |
D. |
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,只需把
的图象,只需把 的图象上所有点( )个单位长度.
的图象上所有点( )个单位长度.

A.向右平移 |
B.向右平移 |
C.向左平移 |
D.向左平移 |
设 是奇函数,且在
是奇函数,且在 是增函数,又
是增函数,又 ,则
,则 的解集是( )
的解集是( )
A. |
B. |
C. |
D. |
已知平面向量 ,且
,且 与
与 反向,则
反向,则 等于( )
等于( )
A. |
B. 或 或 |
C. |
D. |
已知锐角 满足
满足 ,,则
,,则 = ( )
= ( )
A. |
B. π π |
C. 或 或 π π |
D. |
方程 的实数解落在的区间是( )
的实数解落在的区间是( )
A. |
B. |
C. |
D. |
函数 和函数
和函数 (a>0,且a
(a>0,且a 0)的图象画在同一个坐标系中,得到的图象只可能是下面四个图象中的( )
0)的图象画在同一个坐标系中,得到的图象只可能是下面四个图象中的( )

在 所在平面内有一点P,如果
所在平面内有一点P,如果 ,那么
,那么 与
与 面积之比为
面积之比为
A. |
B. |
C. |
D. |
设 ,
, ,且
,且 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. |
B. |
C. |
D. |
定义在实数集 上的函数
上的函数 的图像是连续不断的,若对任意的实数
的图像是连续不断的,若对任意的实数 ,存在常数
,存在常数 使得
使得 恒成立,则称
恒成立,则称 是一个“关于
是一个“关于 函数”,下列“关于
函数”,下列“关于 函数”的结论正确的是( )
函数”的结论正确的是( )
A. 不是 “关于 不是 “关于 函数” 函数” |
B. 是一个“关于 是一个“关于 函数” 函数” |
C.“关于 函数”至少有一个零点 函数”至少有一个零点 |
D. 不是一个“关于 不是一个“关于 函数” 函数” |
已知向量 ,则
,则 =
=
已知 ,则
,则 的值为
的值为
函数 在
在 上为增函数,则实数
上为增函数,则实数 的取值范围是__________.
的取值范围是__________.
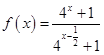 ,则
,则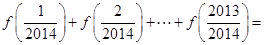 .
.
(本小题满分12分)化简下列各式:
(1)
(2)
(本小题满分12分)二次函数 满足
满足 且
且 .
.
(1)求 的解析式;
的解析式;
(2)在区间 上,
上, 的图象恒在
的图象恒在 的图象上方,试确定实数m的范围.
的图象上方,试确定实数m的范围.
(本小题满分12分)平面内给定三个向量
(1)求满足 的实数
的实数 、
、 ;
;
(2)设 满足
满足 且
且 ,求
,求 .
.
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)求函数 在
在 上的最小值.
上的最小值.
(本小题满分12分)已知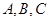 三点的坐标分别为
三点的坐标分别为 ,其中
,其中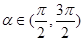
(1)若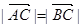 ,求角
,求角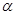 的值;
的值;
(2)若 的值。
的值。
(本小题满分12分)已知定义域为 的函数
的函数 满足:
满足:
① 时,
时, ;
;
② ;
;
③对任意的正实数 ,都有
,都有 ;
;
(1)求证: ;
;
(2)求证: 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式 的解集.
的解集.