已知U={y| },P={y|
},P={y| },则∁UP=( )
},则∁UP=( )
A. |
B. |
C. |
D. ∪ ∪ |
已知角α的终边与单位圆相交于点P(sin ,cos
,cos ),则sinα=( )
),则sinα=( )
A.﹣ |
B.﹣ |
C. |
D. |
如图,点 是线段
是线段 的中点,
的中点, ,且
,且 ,则
,则 ( )
( )

A. |
B. |
C. |
D. |
 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,则下列各式一定成立的( )
,则下列各式一定成立的( )
A. |
B. |
C. |
D. |
设 ,则( )
,则( )
A. |
B. |
C. |
D. |
将函数 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 ( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 ( )
A. |
B.  |
C.  |
D. |
已知 ,
, ,且
,且 ,则
,则 与
与 夹角的余弦值为( )
夹角的余弦值为( )
A. |
B. |
C. |
D. |
函数 的图像关于( )
的图像关于( )
| A.原点对称 | B. 轴对称 轴对称 |
C. 轴对称 轴对称 |
D.直线 对称 对称 |
设偶函数 对任意
对任意 都有
都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
| A.10 | B. |
C.-10 | D. |
若曲线 ,与直线
,与直线 有两个不同的交点,则实数
有两个不同的交点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设函数f(x)=sin(-2x+φ)(0<φ<π),y=f(x)图象的一条对称轴是直线x= .则φ=
.则φ=
如果指数函数 在
在 上的最大值与最小值的差为
上的最大值与最小值的差为 ,则实数
,则实数 _________.
_________.
若 ,则
,则 ,则
,则 的值为_________.
的值为_________.
如果函数 的零点所在的区间是
的零点所在的区间是 ,则正整数
,则正整数 __________.
__________.
定义 (
( 为
为 与
与 的夹角),给出下列命题.
的夹角),给出下列命题.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤设 ,则
,则
其中正确的序号为 .
(本小题满分12分) 已知集合 ,集合
,集合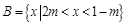 .
.
(1)当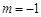 时,求
时,求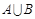 ;
;
(2)若 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若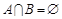 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分13分)如图,以Ox为始边作角α与β( ) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为(
) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为( ,
, ).
).
(1)求 的值;
的值;
(2)若 ·
· ,求
,求 .
.
(本小题满分12分)学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数 与听课时间
与听课时间 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当
时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当 时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳。
时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳。
(1)试求 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由。
(本小题满分12分)设函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当 时,
时, 的最大值为2,求
的最大值为2,求 的值,并求出
的值,并求出 的对称轴方程.
的对称轴方程.
(本小题满分12分)已知函数 图象的一部分如图所示.
图象的一部分如图所示.
(1)求函数 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
(本小题满分14分)已知函数 ,若在区间
,若在区间 内有且仅有一个
内有且仅有一个 ,使得
,使得 成立,则称函数
成立,则称函数 具有性质
具有性质 .
.
(1)若 ,判断
,判断 是否具有性质
是否具有性质 ,说明理由;
,说明理由;
(2)若函数 具有性质
具有性质 ,试求实数
,试求实数 的取值范围.
的取值范围.