已知集合 则满足
则满足 的非空集合
的非空集合 的个数是( )
的个数是( )
| A.1 | B.2 | C.7 | D.8 |
如图,以Ox为始边作任意角α,β,它们的终边与单位圆分别交于A,B点,则 的值等于( )
的值等于( )

| A.sin(α+β) | B.sin(α﹣β) | C.cos(α+β) | D.cos(α﹣β) |
若奇函数 在
在 上为增函数,且有最大值2,则它在
上为增函数,且有最大值2,则它在 上( )
上( )
| A.是减函数,有最小值2 |
| B.是增函数,有最小值-2 |
| C.是减函数,有最大值-2 |
| D.是增函数,有最大值2 |
函数
 的部分图象如图所示,若
的部分图象如图所示,若 ,且
,且 (
( ),则
),则 ( )
( )

| A.1 | B. |
C. |
D. |
函数 的值域是 ( )
的值域是 ( )
| A.R | B. |
C.(2,+∞) | D.(0,+∞) |
 ,若
,若 ,则
,则 的值为( )
的值为( )
| A.-12 | B.-14 | C.12 | D.14 |
已知函数 向左平移
向左平移 个单位后,得到函数
个单位后,得到函数 ,下列关于
,下列关于 的说法正确的是( )
的说法正确的是( )
A.图象关于点 中心对称 中心对称 |
B.图象关于 轴对称 轴对称 |
C.在区间 单调递增 单调递增 |
D.在 单调递减 单调递减 |
函数f(x)的部分图象如图所示,则函数f(x)的解析式可以是( )

| A.f(x)=x-s1n x |
B.f(x)= |
| C.f(x)=2xcos x |
D.f(x)=x·(|x|- )·(|x|- )·(|x|- ) ) |
已知点 若向量
若向量 与
与 同向,
同向, ,则点B的坐标为 .
,则点B的坐标为 .
函数 的单调递增区间为______________.
的单调递增区间为______________.
已知 则
则 _____________.
_____________.
含有三个实数的集合既可表示成 ,又可表示成
,又可表示成 ,则
,则 .
.
设全集为R,集合 ,
, .
.
(1)求 ;
;
(2)已知 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
已知点 ,
, ,点
,点 在单位圆上.
在单位圆上.
(1)若 (
( 为坐标原点),求
为坐标原点),求 与
与 的夹角;
的夹角;
(2)若 ,求点
,求点 的坐标.
的坐标.
已知向量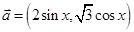 ,
,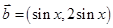 ,函数
,函数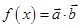
(1)求 的单调递增区间;
的单调递增区间;
(2)若不等式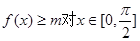 都成立,求实数m的最大值.
都成立,求实数m的最大值.
定义在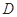 上的函数
上的函数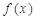 ,如果满足:对任意
,如果满足:对任意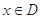 ,存在常数
,存在常数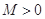 ,都有
,都有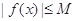 成立,则称
成立,则称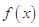 是
是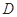 上的有界函数,其中
上的有界函数,其中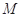 称为函数
称为函数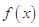 的上界.已知函数
的上界.已知函数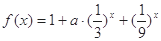 ,
,
(1)当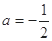 时,求函数
时,求函数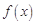 在
在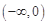 上的值域,并判断函数
上的值域,并判断函数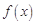 在
在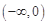 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数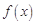 在
在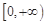 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数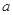 的取值范围.
的取值范围.