已知全集U={小于10的正整数},集合M={3,4,5},P={1,3,6,9},则集合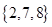 =( )
=( )
A. |
B.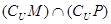 |
C.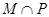 |
D.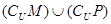 |
下列说法中正确的是( )
| A.棱柱的面中,至少有两个面互相平行 |
| B.棱柱的两个互相平行的平面一定是棱柱的底面 |
| C.棱柱的一条侧棱的长叫做棱柱的高 |
| D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形 |
函数 的定义域是( )
的定义域是( )
A.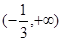 |
B.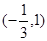 |
C.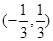 |
D.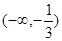 |
如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( )
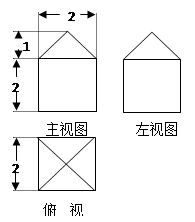
A. |
B.21 |
C.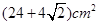 |
D.24 |
若直线 与
与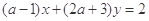 互相垂直,则a等于( )
互相垂直,则a等于( )
| A.3 | B.1 | C.0或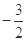 |
D.1或-3 |
对于平面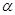 、
、 、
、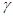 和直线
和直线 、
、 、
、 、
、 ,下列命题中真命题是( )
,下列命题中真命题是( )
A.若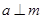 , , , ,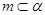 , , ,则 ,则 |
B.若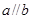 , , ,则 ,则 |
C.若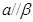 , ,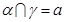 , ,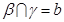 ,则 ,则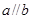 |
D.若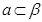 , ,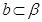 , ,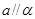 , , ,则 ,则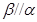 |
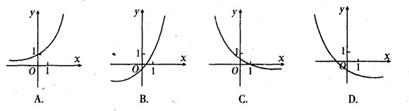
函数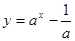
 的图象可能是( )
的图象可能是( )
过点(3,1)作圆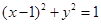 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )
A. |
B.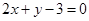 |
C.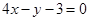 |
D. |
对于函数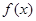 中任意的
中任意的 有如下结论:
有如下结论:
①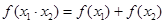 ;
;
②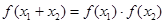 ;
;
③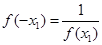 ;
;
④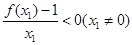 ;
;
⑤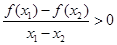 .
.
当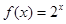 时,上述结论中正确结论的个数是( )
时,上述结论中正确结论的个数是( )
| A.2个 | B.3个 | C.4个 | D.5个 |
已知P是直线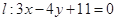 上的动点,PA、PB是圆
上的动点,PA、PB是圆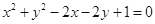 的两条切线,C是圆心,那么四边形PACB面积的最小值( )
的两条切线,C是圆心,那么四边形PACB面积的最小值( )
A.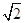 B.2
B.2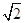 C.
C.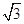 D.2
D.2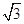
过点 的直线
的直线 被圆
被圆 所截得的弦长为10,则直线
所截得的弦长为10,则直线 的方程为 .
的方程为 .
一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为 .
设函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, ,则不等式
,则不等式 的解集用区间表示为_________.
的解集用区间表示为_________.
函数 的值域是 .
的值域是 .
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有 个.

(本小题满分12分)已知全集 ,集合
,集合 ,
, ,
, .
.
(1)求 ,
, ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在三棱锥 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
(本小题满分12分)已知圆 ,直线
,直线 ,
, 。
。
(1)证明:不论 取什么实数,直线
取什么实数,直线 与圆恒交于两点;
与圆恒交于两点;
(2)求直线被圆 截得的弦长最小时
截得的弦长最小时 的方程.
的方程.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
(1)求证:平面 平面
平面 ;
;
(2)当 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出 的值.
的值.
(本小题满分13分)设函数 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
(1)求 的值;
的值;
(2)判断函数 的奇偶性;
的奇偶性;
(3)如果 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分) 在平面直角坐标系 中,已知圆
中,已知圆 过坐标原点O且圆心在曲线
过坐标原点O且圆心在曲线 上.
上.
(1)若圆M分别与 轴、
轴、 轴交于点
轴交于点 、
、 (不同于原点O),求证:
(不同于原点O),求证: 的面积为定值;
的面积为定值;
(2)设直线 与圆M 交于不同的两点C,D,且
与圆M 交于不同的两点C,D,且 ,求圆M的方程;
,求圆M的方程;
(3)设直线 与(2)中所求圆M交于点
与(2)中所求圆M交于点 、
、 ,
,  为直线
为直线 上的动点,直线
上的动点,直线 ,
, 与圆M的另一个交点分别为
与圆M的另一个交点分别为 ,
, ,求证:直线
,求证:直线 过定点.
过定点.