若复数 (a∈R,i是虚数单位)是纯虚数,则a的值为________.
(a∈R,i是虚数单位)是纯虚数,则a的值为________.
若一个圆锥的侧面展开图是面积为 的半圆面,则该圆锥的体积为________.
的半圆面,则该圆锥的体积为________.
已知 ,则
,则 .
.
设偶函数 的定义域为
的定义域为 ,
, 在区间
在区间 上为增函数,则
上为增函数,则 的大小关系是 .
的大小关系是 .
现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、
导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事
其他三项工作,丙、丁、戊都能胜四项工作,则不同安排方案的种数是 。
已知函数 ,则
,则 ____________.
____________.
若a、b为实数,则“0<ab<1”是“b< ”的________条件.
”的________条件.
设无穷等比数列{ }的公比为q,若
}的公比为q,若 ,则q= 。
,则q= 。
双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则
,则 _________.
_________.
 展开式中的常数项为___________.
展开式中的常数项为___________.
若 ,则向量
,则向量 与
与 的夹角为___________.
的夹角为___________.
已知数列{an}满足an=an-1+n-1(n≥2,n∈N),一颗质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子连续抛掷三次,得到的点数分别记为a,b,c,则满足集合{a,b,c}={a1,a2,a3}(1≤ai≤6,i=1,2,3)的概率是 .
若关于x的不等式ax2+x-2a<0的解集中仅有4个整数解,则实数a的取值范围为 .
设正实数x,y,z满足x2-3xy+4y2-z=0,则当 取得最大值时,
取得最大值时, 的最大值为 。
的最大值为 。
函数 ,
, 是( )
是( )
A.最小正周期为 的奇函数 的奇函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的偶函数 的偶函数 |
两个实习生每人加工一个零件.加工为一等品的概率分别为 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A. |
B. |
C. |
D. |
若以直角坐标系的原点为极点, 轴的非负半轴为极轴建立极坐标系,则线段
轴的非负半轴为极轴建立极坐标系,则线段 的极坐标为( )
的极坐标为( )
A. |
B. |
C. |
D. |
已知等差数列 中,
中, 是前n项和
是前n项和 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
给定函数
(1)求 ;
;
(2)判断 的奇偶性,并证明你的结论。
的奇偶性,并证明你的结论。
(本题满分14分) 本题有2个小题,第一小题满分6分,第二小题满分8分。
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.

(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
本题共有2个小题,第1小题满分5分,第2小题满分9分.
为进行科学实验,观测小球A、B在两条相交成 角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道
角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道 按箭头的方向运动。问:(1)运动开始前,A、B的距离是多少米?(结果保留三位有效数字,参考数据:
按箭头的方向运动。问:(1)运动开始前,A、B的距离是多少米?(结果保留三位有效数字,参考数据:


 )。
)。
几分钟后,两个小球的距离最小?
本题共3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知动圆 过点
过点 并且与圆
并且与圆 相外切,动圆圆心
相外切,动圆圆心 的轨迹为
的轨迹为 ,轨迹
,轨迹 与
与 轴的交点为
轴的交点为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)设直线 过点
过点 且与轨迹
且与轨迹 有两个不同的交点
有两个不同的交点 ,求直线
,求直线 斜率
斜率 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若 ,证明直线
,证明直线 过定点,并求出这个定点的坐标.
过定点,并求出这个定点的坐标.
本题共3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分.
已知数列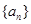 ,
,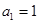 ,
,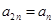 ,
,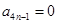 ,
,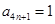
 .
.
(Ⅰ)求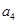 ,
, ;
;
(Ⅱ)是否存在正整数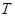 ,使得对任意的
,使得对任意的 ,有
,有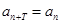 ;
;
(Ⅲ)设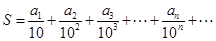 ,问
,问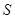 是否为有理数,说明理由.
是否为有理数,说明理由.