已知复数
 (
( 为虚数单位),则复数
为虚数单位),则复数 为( )
为( )
A. |
B. |
C. |
D. |
若 ,且
,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
已知平面向量 ,
, ,
, 与
与 垂直,则
垂直,则 是( )
是( )
| A.-1 | B.1 | C.-2 | D.2 |
执行如图所示的程序框图,则输出的 值等于( )
值等于( )

A. |
B. |
C. |
D. |
等比数列 的前
的前 项和为
项和为 ,
, ,若
,若 成等差数列,则
成等差数列,则 ( )
( )
| A.7 | B.8 | C.16 | D.15 |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, 则
则 等于( )
等于( )
A. |
B. |
C. |
D. |
某几何体的三视图如图所示,则该几何体的体积为( )

| A.240 | B.200 | C. |
D. |
若双曲线 的离心率为2,则其渐近线的斜率为( )
的离心率为2,则其渐近线的斜率为( )
A. |
B. |
C. |
D. |
若变量 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
若函数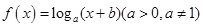 的大致图象如右图所示,则函数
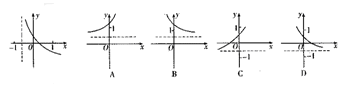
的大致图象如右图所示,则函数 的大致图象为( )
的大致图象为( )
若正数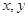 满足
满足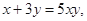 则
则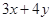 的最小值是( )
的最小值是( )
A.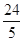 |
B. |
C.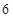 |
D.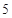 |
命题“ ”的否定是: .
”的否定是: .
函数 的最小正周期为 。
的最小正周期为 。
设 ,函数
,函数 ,则
,则 的值等于 .
的值等于 .
若f(x)= 是R上的单调函数,则实数a的取值范围为 .
是R上的单调函数,则实数a的取值范围为 .
(本小题满分12分)在 中,角
中,角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
.
(Ⅰ)若 ,
, ,求
,求 的值;
的值;
(Ⅱ)若 ,求
,求 的最大值.
的最大值.
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
, ,
, ,
, 平面
平面 ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)若 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.
(本小题满分12分)某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表:
| 分组 |
频数 |
频率 |
| [0,1) |
25 |
y |
| [1,2) |
|
0.19 |
| [2,3) |
50 |
x |
| [3,4) |
|
0.23 |
| [4,5) |
|
0.18 |
| [5,6] |
5 |
|

(Ⅰ)分别求出x,n,y的值;
(Ⅱ)若从样本中月均用水量在[5,6]内的5位居民a,b,c,d,e中任选2人作进一步的调查研究,求居民a被选中的概率.
(本小题满分12分)已知 分别为椭圆
分别为椭圆 :
: (
( )的左、右焦点, 且离心率为
)的左、右焦点, 且离心率为 ,点
,点 椭圆
椭圆 上。
上。
(1)求椭圆 的方程;
的方程;
(2)是否存在斜率为 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,使直线
,使直线 与
与 的倾斜角互补,且直线
的倾斜角互补,且直线 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
(本小题满分12分)已知函数 (其中
(其中 为常数且
为常数且 )在
)在 处取得极值.
处取得极值.
(I) 当 时,求
时,求 的单调区间;
的单调区间;
(II) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
(本小题满分10)选修4—1:几何证明选讲
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD .
(1)求证:DE是圆O的切线;
(2)如果AD ="AB" = 2,求EB的长.
(本小题满分10)选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线 ,已知过点
,已知过点 的直线的参数方程为:
的直线的参数方程为: (t为参数),直线与曲线C分别交于M,N.
(t为参数),直线与曲线C分别交于M,N.
(1)写出曲线C和直线的普通方程;
(2)若 成等比数列,求a的值.
成等比数列,求a的值.
(本小题满分10)选修4-5:不等式选讲
已知 .
.
(1)解不等式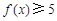 ;
;
(2)若关于x的不等式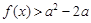 对任意的
对任意的 恒成立,求a的取值范围.
恒成立,求a的取值范围.