不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
(理科做)已知点A(-3,1,4),则点A关于x轴的对称点的坐标为( )
A、(-3,1,-4) B、(3,-1,-4)
C、(-3,-1,-4) D、(-3,,1,-4)
(文科做)曲线 在点(-1,-3)处的切线方程是( )
在点(-1,-3)处的切线方程是( )
A. B.
B.
C. D.
D.
设等比数列 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
已知双曲线 的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
A. |
B. |
C. |
D. |
若 为等差数列,
为等差数列, 是其前
是其前 项和,且S15 =
项和,且S15 = ,则tan
,则tan 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D. |
在 中,若
中,若 ,则
,则 为
为
| A.直角三角形 | B.等腰三角形 |
| C.等腰直角三角形 | D.等腰三角形或直角三角形 |
有下列四个命题:
①命题“若 ,则
,则 ,
, 互为倒数”的逆命题;
互为倒数”的逆命题;
②命题“面积相等的三角形全等”的否命题;
③命题“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④命题“若 ,则
,则 ”的逆否命题.
”的逆否命题.
其中是真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列且c=2a,则 = ( )
= ( )
A. B.
B. C.
C. D.
D.
直线 经过椭圆
经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率为( )
的一个焦点和一个顶点,则该椭圆的离心率为( )
A. |
B. |
C. |
D. |
设 若
若 是
是 与
与 的等比中项,则
的等比中项,则 的最小值为 ( )
的最小值为 ( )
| A.8 | B.4 | C.1 | D. |
已知抛物线 ,以
,以 为中点作抛物线的弦,则这条弦所在直线的方程为
为中点作抛物线的弦,则这条弦所在直线的方程为
A. |
B. |
C. |
D. |
设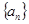 是等比数列,公比
是等比数列,公比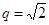 ,
,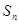 为
为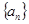 的前n项和。记
的前n项和。记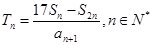 ,设
,设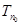 为数列
为数列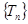 的最大项,则
的最大项,则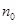 =( )
=( )
| A.3 | B.4 | C.5 | D.6 |
命题“ ,
,  ”的否定是 .
”的否定是 .
椭圆 的焦距为6,则
的焦距为6,则 = .
= .
(理科做)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).则以 为边的平行四边形的面积为________.
为边的平行四边形的面积为________.
(文科做)已知直线 与
与 在点
在点 处的切线互相垂直,则
处的切线互相垂直,则 .
.
已知变量 满足约束条件
满足约束条件 若目标函数
若目标函数 仅在点
仅在点 处取得最大值,则实数
处取得最大值,则实数 的取值范围是 .
的取值范围是 .
(本小题满分10分)设p:实数 满足
满足 (其中
(其中 ),q:实数x满足
),q:实数x满足
(1)若 ,且p∧q为真,求实数
,且p∧q为真,求实数 的取值范围;
的取值范围;
(2)若p是q的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题共12分)△ABC的三个内角A,B,C的对边分别为a,b,c,且△ABC的面积为 .
.
(1)若 ,求角A,B,C的大小;
,求角A,B,C的大小;
(2 )若a=2,且 ,求边c的取值范围.
,求边c的取值范围.
(本小题满分12分)已知双曲线 的离心率为
的离心率为 ,点
,点 是双曲线的一个顶点.
是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过的双曲线右焦点 作倾斜角为30°直线
作倾斜角为30°直线 ,直线
,直线 与双曲线交于不同的
与双曲线交于不同的 两点,求
两点,求 的长.
的长.
(本小题满分12分)各项均不相等的等差数列 的前四项的和为
的前四项的和为 ,且
,且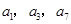 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式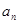 与前n项和
与前n项和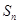 ;
;
(2)记 为数列
为数列 的前n项和,求
的前n项和,求
(本小题满分12分)(理科做)在四棱锥P-ABCD中,侧面PCD 底面ABCD,PD
底面ABCD,PD CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC,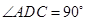 ,
, ,
,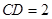 .
.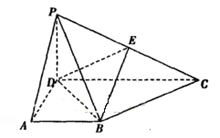
(1)求证:BC 平面PBD:
平面PBD:
(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点,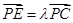 ,试确定
,试确定 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为 .
.
(文科做)已知函数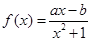 在点
在点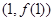 的切线方程为
的切线方程为 .
.
(1)求函数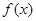 的解析式;
的解析式;
(2)设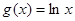 ,求证:
,求证: 在
在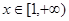 上恒成立.
上恒成立.
(本小题满分12分)设椭圆 的左右焦点分别为
的左右焦点分别为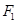 、
、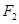 ,
,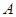 是椭圆
是椭圆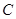 上的一点,
上的一点,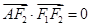 ,坐标原点
,坐标原点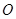 到直线
到直线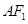 的距离为
的距离为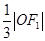 .
.
(1)求椭圆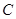 的方程;
的方程;
(2)设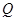 是椭圆
是椭圆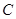 上的一点,
上的一点,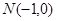 ,连接QN的直线交
,连接QN的直线交 轴于点
轴于点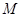 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.