若2x=3y，则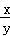
的值为（ ）
A． |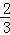
B． |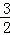
C． |
D． |
二次函数y=2（x+1）2﹣3的最小值是（ ）
| A．1 | B．﹣1 | C．3 | D．﹣3 |
对甲、乙两同学100米短跑进行5次测试，通过计算，他们成绩的平均数相等，方差S2甲=0.025，S2乙=0.246，下列说法正确的是（ ）
| A．甲短跑成绩比乙好 | B．乙短跑成绩比甲好 |
| C．甲比乙短跑成绩稳定 | D．乙比甲短跑成绩稳定 |
在平面直角坐标系中，将函数y=2x2的图象先向右平移1个单位，再向上平移5个单位得到图象的函数关系式是（ ）
| A．y=2（x﹣1）2﹣5 | B．y=2（x﹣1）2+5 |
| C．y=2（x+1）2﹣5 | D．y=2（x+1）2+5 |
如图，⊙O的直径AB=12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP：AP=1：5，则CD的长为（ ）
A．4 |
B．8 |
C．2 |
D．4 |
若圆锥的底面半径为3cm，母线长为5cm，则圆锥的侧面积是（ ）
| A．15cm2 | B．30cm2 | C．15лcm2 | D．30лcm2 |
如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于C点，连接BC，若∠A=30°，
，则AC等于（ ）
| A．4 | B．6 | C． |
D． |
如图，Rt△ABC中，AC=BC=2，正方形CDEF的顶点D、F分别在AC、BC边上，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系的是（ ）
A． 
B．
C．
D．
要使式子
有意义，则a的取值范围为 ．
化去根号内的分母：
= ．
若关于x的一元二次方程（m+3）x2+5x+m2+2m﹣3=0有一个根为0，则m= ，另一根为 ．
方程x2﹣3x﹣10=0的两根之比为 ．
已知方程x2﹣7x+12=0的两根恰好是Rt△ABC的两条边的长，则Rt△ABC的第三边长为 ．
一个两位数，个位数比十位数大3，且个位数的平方等于这个两位数，这个两位数为 ．
某超市从我国西部某城市运进两种糖果，甲种a千克，每千克x元，乙种b千克，每千克y元，如果把这两种糖果混合后销售，保本价是 元/千克．
已知AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连结AC，若∠CAB=30°，则∠ADC= ．
计算：
×
﹣（
+
）
解方程：2x2+5x=3．
已知方程2（m+1）x2+4mx+3m=2，根据下列条件之一求m的值．
（1）方程有两个相等的实数根；
（2）方程有两个相反的实数根；
（3）方程的一个根为0．
已知x1、x2是一元二次方程2x2﹣2x+m+1=0的两个实根．
（1）求实数m的取值范围；
（2）如果m满足不等式7+4x1x2＞x12+x22，且m为整数．求m的值．
如图，某建筑工程队利用一面墙（墙的长度不限），用40米长的篱笆围成一个长方形的仓库．
（1）求长方形的面积是150平方米，求出长方形两邻边的长；
（2）能否围成面积220平方米的长方形？请说明理由．
有100米长的篱笆材料，想围成一个矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长为50米的旧墙，有人用这个篱笆围成一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求，现请你设计矩形仓库的长和宽，使它符合要求．
如图，在△ABC中，AB=AC，⊙O是△ABC的内切圆，它与AB，BC，CA分别相切于点D、E、F．
（1）求证：BE=CE；
（2）若∠A=90°，AB=AC=2，求⊙O的半径．
如图，给出了我国从1998年～2002年每年教育经费投入的情况．
（1）由图可见，1998年～2002年这五年内，我国教育经费投入呈现出 趋势；
（2）根据图中所给数据，求我国1998年～2002年教育经费的年平均数；
（3）如果我国的教育经费从2002年的5480亿元增加到2004年的7891亿元，那么这两年的教育经费平均增长率为多少？（结果精确到0.01）
已知抛物线y=x2﹣2x﹣
与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C．
（1）点A的坐标为 ，点C的坐标为 ；
（2）在y轴的正半轴上是否存在点P，使以点P，O，A为顶点的三角形与△AOC相似？若存在，求出点P的坐标，若不存在，请说明理由．
已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF交于点G．
（1）如图1，若四边形ABCD是矩形，且DE⊥CF．则DE•CD CF•AD（填“＜”或“=”或“＞”）；
（2）如图2，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得DE•CD=CF•AD成立？并证明你的结论；
（3）如图3，若BA=BC=3，DA=DC=4，∠BAD=90°，DE⊥CF．则
的值为 ．
（1）在Rt△ABC中，∠C=90°，∠B=30°．
①△ABC绕点C顺时针旋转得到△DEC，点D恰好落在AB边上．如图1，则S△BDC与S△AEC的数量关系是 ；
②当△DEC绕点C旋转到图2的位置时，小娜猜想①中S△BDC与S△AEC的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小娜的猜想；
（2）已知，∠ABC=60°，点D是∠ABC平分线上一点，BD=CD=2，DE∥AB交BC于点E，如图3．若在射线BA上存在点F，使S△DCF=S△BDE，则BF= ．
定义：把一个半圆与抛物线的一部分合成封闭图形，我们把这个封闭图形称为“蛋圆”．如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，8），AB为半圆的直径，半圆的圆心M的坐标为（1，0），半圆半径为3．
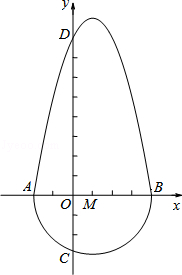
（1）请你直接写出“蛋圆”抛物线部分的解析式y ，自变量的取值范围是 ；
（2）请你求出过点C的“蛋圆”切线与x轴的交点坐标；
（3）求经过点D的“蛋圆”切线的解析式．