命题“对任意 都有
都有 ”的否定是( )
”的否定是( )
A.对任意 ,都有 ,都有 |
B.不存在 ,使得 ,使得 |
C.存在 ,使得 ,使得 |
D.存在 ,使得 ,使得 |

A. |
B. |
C. |
D. |
把1 011(2)化为十进制数为( )
| A.11 | B.12 | C.112 | D.1011 |
程序框图如下图所示,则输出 的值为( )
的值为( )

| A.15 | B.21 | C.22 | D.28 |
双曲线 的实轴长是 ( )
的实轴长是 ( )
| A.2 | B. |
C.4 | D. |
已知 与
与 之间的几组数据如下表:
之间的几组数据如下表:
| X |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则 与
与 的线性回归方程
的线性回归方程 必过( )
必过( )
A. B.
B. C.
C. D.
D.
如图,正方形 是由四个全等的小直角三角形与中间的一个小正方形拼接而成,现随机地向大正方形内部区域投掷小球,若直角三角形的两条直角边的比是2:1,则小球落在小正方形区域的概率是( )
是由四个全等的小直角三角形与中间的一个小正方形拼接而成,现随机地向大正方形内部区域投掷小球,若直角三角形的两条直角边的比是2:1,则小球落在小正方形区域的概率是( )

A. |
B. |
C. |
D. |
(理科做) =( )
=( )
A.1 B.﹣1 C.﹣5 D.5
(文科做)
设函数
 ,曲
,曲 线在点
线在点 处的切线方程为( )
处的切线方程为( )
A. B.
B. C.
C. D.
D.
某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和为( )

| A.117 | B.118 | C.118.5 | D.119.5 |
若样本 的方差是
的方差是 ,则样本
,则样本 的方差为( )
的方差为( )
A.3 +1 +1 |
B.9 +1 +1 |
C.9 +3 +3 |
D.9 |
“数列 (
( )满足
)满足 (其中
(其中 为常数)”是“数列
为常数)”是“数列 (
( )是等比数列”的
)是等比数列”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
已知点A(3,4),F是抛物线y2=8x的焦点,M是抛物线上的动点,当|AM|+|MF|最小时,M点坐标是( )
| A.(0,0) | B.(3,2 ) ) |
C.(2,4) | D.(3,-2 ) ) |
某运动队有男女运动员49人,其中男运动员有28人,按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为14的样本,那么应抽取女运动员人数是 .
已知实数1,m,9构成一个等比数列,则圆锥曲线 +y2=1的离心率为 .
+y2=1的离心率为 .
设 ,
, ,由计算得
,由计算得 ,
, ,
, ,
, ,观察上述结果,可推出一般的结论为 .
,观察上述结果,可推出一般的结论为 .
(理科做)在直三棱柱 中,底面ABC为直角三角形,
中,底面ABC为直角三角形, ,
, . 已知G与E分别为
. 已知G与E分别为 和
和 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和 上的动点(不包括端点). 若
上的动点(不包括端点). 若 ,则线段
,则线段 的长度的最小值为 。
的长度的最小值为 。
(文科做)函数 在
在 内单调递减,则实数a的范围为 .
内单调递减,则实数a的范围为 .
命题 :关于
:关于 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
(本小题12分)已知 ,
, ,点
,点 的坐标为
的坐标为 .
.
(1)求当 时,点
时,点 满足
满足 的概率;
的概率;
(2)求当 时,点
时,点 满足
满足 的概率.
的概率.
(本小题12分)为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题:
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
(本小题12分)在平面直角坐标系中,已知一个椭圆的中心在原点,左焦点为 ,且过
,且过 .
.
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,点
是椭圆上的动点,点 ,求线段
,求线段 中点
中点 的轨迹方程.
的轨迹方程.
(本小题满分12分)(理科做)如图,四棱锥 中,平面
中,平面
 平面
平面 ,
, //
// ,
, ,
, ,且
,且 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求 和平面
和平面 所成角的正弦值;
所成角的正弦值;
(3)在线段 上是否存在一点
上是否存在一点 使得平面
使得平面
 平面
平面 ,请说明理由.
,请说明理由.
(文科做)已知函数 ,其中
,其中 是常数.
是常数.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若存在实数 ,使得关于
,使得关于 的方程
的方程 在
在 上有两个不相等的实数根,求
上有两个不相等的实数根,求 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆 的离心率为
的离心率为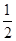 ,直线
,直线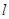 过点
过点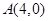 ,
, ,且与椭圆
,且与椭圆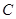 相切于点
相切于点 .
.
(1)求椭圆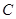 的方程;
的方程;
(2)是否存在过点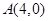 的直线
的直线 与椭圆
与椭圆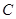 相交于不同的两点
相交于不同的两点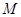 、
、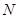 ,使得
,使得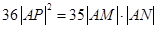 ?若存在,试求出直线
?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.