设集合 ,
, ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
下列四组中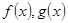 表同一函数的是( )
表同一函数的是( )
A.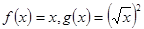 |
B.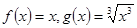 |
C.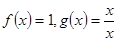 |
D.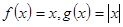 |
若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 ,用二分法求方程
,用二分法求方程 内近似解的过程中取区间中点
内近似解的过程中取区间中点 ,那么下一个有根区间为( )
,那么下一个有根区间为( )
A. |
B. |
C. 或 或 |
D.不能确定 |
函数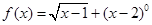 的定义域为( )
的定义域为( )
A. |
B.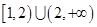 |
C.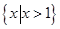 |
D.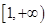 |
下列函数是偶函数的是:( )
A. |
B. |
C. |
D. |
当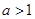 时,在同一坐标系中,函数
时,在同一坐标系中,函数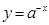 与
与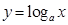 的图象是:( )
的图象是:( )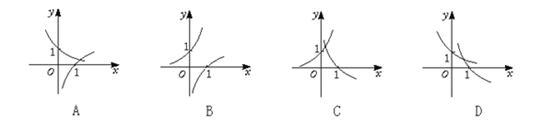
.设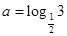 ,
,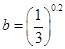 ,
,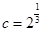 ,则:( )
,则:( )
A.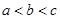 |
B.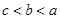 |
C.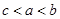 |
D.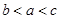 |
函数 在
在 上的最大值与最小值的和为
上的最大值与最小值的和为 ,则函数
,则函数 在
在 的最大值是( ).
的最大值是( ).
A. |
B. |
C. |
D. |
已知函数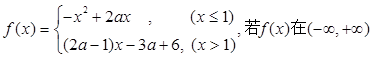 上是增函数,则实数
上是增函数,则实数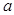 的取值范围是( )
的取值范围是( )
A.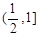 |
B.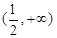 |
C.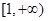 |
D.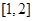 |
已知幂函数 的图象经过点
的图象经过点 ,则该幂函数的解析式为 .
,则该幂函数的解析式为 .
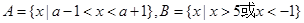 ,且
,且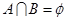 ,则
,则 的取值范围 .
的取值范围 .
函数 的图像恒经过的定点是________.
的图像恒经过的定点是________.
已知定义在 上的函数
上的函数 和
和 ,其图象如下图所示:
,其图象如下图所示:
给出下列四个命题:
程 有且仅有6个根
有且仅有6个根
②方程 有且仅有3个根
有且仅有3个根
③方程 有且仅有5个根
有且仅有5个根
④方程 有且仅有4个根
有且仅有4个根
其中正确的命题是 .(将所有正确的命题序号填在横线上).
已知集合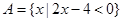 ,
,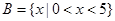 , 全集
, 全集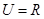 ,求:
,求:
(1)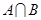 ; (2)
; (2)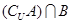 .
.
计算下列各式的值:
(1)
(2)
已知函数 .
.
(1)判断函数 的奇偶性,并加以证明;[来(2)用定义证明函数
的奇偶性,并加以证明;[来(2)用定义证明函数 在区间
在区间 上为增函数.
上为增函数.
已知函数 ,若
,若 ;
;
(1)求 的值; (2)求
的值; (2)求 的值; (3)解不等式
的值; (3)解不等式 .
.
某地上年度电价为 元,年用电量为
元,年用电量为 亿千瓦时.本年度计划将电价调至
亿千瓦时.本年度计划将电价调至 之间,经测算,若电价调至
之间,经测算,若电价调至 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与 元成反比例.又当
元成反比例.又当 时,
时, .
.
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为 元,则电价调至多少时,本年度电力部门的收益将比上年增加
元,则电价调至多少时,本年度电力部门的收益将比上年增加 ?[收益=用电量×(实际电价-成本价)]
?[收益=用电量×(实际电价-成本价)]
(本小题满分14分)已知幂函数 ,且
,且 在
在 上单调递增.
上单调递增.
(1)求实数 的值,并写出相应的函数
的值,并写出相应的函数 的解析式;
的解析式;
(2)若 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)试判断是否存在正数 ,使函数
,使函数 在区间
在区间 上的值域为
上的值域为 .若存在,求出
.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.