要得到函数
的导函数f′（x）的图象，只需将f（x）的图象（ ）
A．向右平移 个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） |
| B．向左平移个单位，再把各点的纵坐标缩短到原来的2倍（横坐标不变） |
C．向右平移 个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） |
| D．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） |
设a∈R，函数f（x）=ex+a•e﹣x的导函数是f′（x），且f′（x）是奇函数．若曲线y=f（x）的一条切线的斜率是
，则切点的横坐标为（ ）
| A．ln2 | B．﹣ln2 | C． |
D． |
已知
，将函数
的图象按向量
平移后，所得图象恰好为函数y=﹣f′（x）（f′（x）为f（x）的导函数）的图象，则c的值可以为（ ）
A． |
B．π | C． |
D． |
已知函数f（x）=
，要得到
f′（x）的图象，只需将f（x）的图象（ ）个单位．
A．向右平移 |
B．向左平移 |
C．向右平移 |
D．向左平移 |
已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＞f（x）g′（x），且f（x）=ax•g（x）（a＞0，且a≠1），
．，若数列
的前n项和大于62，则n的最小值为（ ）
| A．6 | B．7 | C．8 | D．9 |
已知曲线y=
x2的一条切线的斜率为
，则切点的横坐标为（ ）
| A．4 | B．3 | C．2 | D． |
已知f（x），g（x）都是定义在R上的函数，且
（a＞0，且a≠1），f′（x）g（x）＜f（x）g′（x），
，则a的值为（ ）
| A．2 | B． |
C． |
D． |
设函数f（x）=g（x）+x+lnx，曲线y=g（x）在点（1，g（1））处的切线方程为y=2x+1，则曲线y=f（x）在点（1，f（1））处的切线方程为（ ）
| A．y=4x | B．y=4x﹣8 | C．y=2x+2 | D． |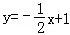
设f（x）=cos22x，则
=（ ）
| A．2 | B． |
C．﹣1 | D．﹣2 |
已知y=f（x）=ln|x|，则下列各命题中，正确的命题是（ ）
A．x＞0时，f′（x）= ，x＜0时，f′（x）=﹣ |
| B．x＞0时，f′（x）=，x＜0时，f′（x）无意义 |
| C．x≠0时，都有f′（x）= |
| D．∵x=0时f（x）无意义，∴对y=ln|x|不能求导 |
为得到函数y=sin（2x+
）的导函数图象，只需把函数y=sin2x的图象上所有点的（ ）
A．纵坐标伸长到原来的2倍，横坐标向左平移 |
B．纵坐标缩短到原来的 倍，横坐标向左平移 |
C．纵坐标伸长到原来的2倍，横坐标向左平移 |
D．纵坐标缩短到原来的 倍，横坐标向左平移 |
已知函数f（x）=cos（x+ϕ）（0＜ϕ＜π）的导函数f'（x）的图象如图所示，则ϕ=（ ）
A． |
B． |
C． |
D． |
函数y=sin（2x2+x）导数是（ ）
| A．y′=cos（2x2+x） |
| B．y′=2xsin（2x2+x） |
| C．y′=（4x+1）cos（2x2+x） |
| D．y′=4cos（2x2+x） |
函数f（x）=sin2x的导数f′（x）=（ ）
| A．2sinx | B．2sin2x | C．2cosx | D．sin2x |
曲线f（x）=lnx+2x在点（1，f（1））处的切线方程是（ ）
| A．3x﹣y+1=0 | B．3x﹣y﹣1=0 | C．3x+y﹣1=0 | D．3x﹣y﹣5=0 |
已知函数f（x﹣1）=2x2﹣x，则f′（x）=（ ）
| A．4x+3 | B．4x﹣1 | C．4x﹣5 | D．4x﹣3 |
函数
的导数为（ ）
A． |
B． |
C． |
D． |
下列求导运算正确的是（ ）
A． |
B． |
| C．（（2x+3）2）′=2（2x+3） |
| D．（e2x）′=e2x |
设f（x）=sinxcosx，那么f′（x）=（ ）
| A．﹣cosxsinx | B．cos2x | C．sinx+cosx | D．cosx﹣sinx |
若函数f（x）=
，则f′（x）是（ ）
| A．仅有最小值的奇函数 |
| B．仅有最大值的偶函数 |
| C．既有最大值又有最小值的偶函数 |
| D．非奇非偶函数 |