若集合
，且
，则集合
可能是（ ）
A． |
B． |
C． |
D． |
已知
为虚数单位，复数
,
＝（ ）
| A．1 | B． |
C． |
D．3 |
下列函数中，在定义域上既是奇函数又存在零点的函数是（ ）．
A． |
B． |
C． |
D． |
已知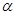
为第二象限角，
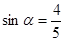，则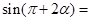
（ ）
A． |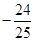
B． |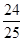
C． |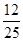
D． |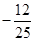
阅读程序框图，运行相应的程序，则输出
的值为（ ）
A． |
B． |
C． |
D． |
已知两条直线
，两个平面
．给出下面四个命题：（ ）
①
；
②
；
③
；
④
．
其中正确的命题序号为 （ ）
| A．①② | B．②③ | C．①④ | D．②④ |
如图是一容量为
的样本的重量的频率分布直方图，则由图可估计样本的平均重量为（ ）
A． |
B． |
C． |
D． |
设变量
，
满足约束条件
，则
的最大值为（ ）
A． |
B．4 | C．3 | D． |
过双曲线
的右焦点
作垂直于
轴的直线，交双曲线的渐近线于
两点，若
（
为坐标原点）是等边三角形，则双曲线的离心率为 （ ）
A． |
B． |
C． |
D． |
记
表示不超过
的最大整数，例如
，
．函数
，在
时恒有
，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
设
，向量
，
，且
，则
___________．
设曲线
在点
处的切线与直线
垂直，则
————．
已知各项都是正数的等比数列
满足
，若存在不同的两项
和
，使得
，则
的最小值是__________．
（坐标系与参数方程选做题）在极坐标系中，圆
＝4cos
的圆心到直线
的距离是 ．
（几何证明选讲选做题）如图，在半圆
中，
是圆上一点，
直径
，垂足为
，
，垂足为
，若
，
，则
．
已知函数
（1）求函数
的最小正周期和最大值；
（2）设
的三内角分别是A、B、C．若
，且
,求边
和
的值．
汽车是碳排放量比较大的行业之一，某地规定，从2015年开始，将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税．检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下（单位：g/km）．
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为
．
（1）求表中
的值，并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
（2）从被检测的5辆甲品牌轻型汽车中任取2辆，则至少有一辆二氧化碳排放量超过
的概率是多少？
如图，
是边长为
的正方形，
是矩形，平面
平面,
为
的中点．
（1）求证：
//平面
；
（2）若三棱锥
的体积为
，求三棱柱
的体积．
已知数列
满足
，
．
（1）求证：数列
是等差数列；
（2）设
，数列
的前
项之和为
，求证：
．
设
、
是焦距等于
的椭圆
的左、右顶点，曲线
上的动点
满足
，其中
和
分别是直线
、
的斜率．
（1）求曲线的方程；
（2）直线
与椭圆
只有一个公共点且交曲线于
两点，若以线段为直径的圆过点，求直线的方程．
已知函数
，
,
．
（1）若函数
在区间
内恰有两个零点，求实数
的取值范围；
（2）若
，设函数在区间
上的最大值为
，最小值为
,记
,求函数
在区间
上的最小值．