若集合 ,
, R
R ,则
,则 .
.
若 ,则常数
,则常数 .
.
若 ,则函数
,则函数 的最小值为 .
的最小值为 .
函数 的单调递减区间是 .
的单调递减区间是 .
方程 的解集为 .
的解集为 .
如图,正三棱柱的底面边长为 ,体积为
,体积为 ,则直线
,则直线 与底面
与底面 所成的角的大小为 (结果用反三角函数值表示).
所成的角的大小为 (结果用反三角函数值表示).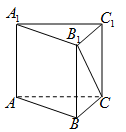
若方程 表示双曲线,则实数
表示双曲线,则实数 的取值范围是 .
的取值范围是 .
函数 (
( )的反函数是 .
)的反函数是 .
在二项式 的展开式中,含
的展开式中,含 项的系数为 (结果用数值表示).
项的系数为 (结果用数值表示).
若抛物线 (
( )的焦点在圆
)的焦点在圆 内,则实数
内,则实数 的取值范围是 .
的取值范围是 .
在 中,三个内角
中,三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,
,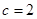 ,
, ,则
,则 .
.
若无穷等比数列 的各项和等于公比
的各项和等于公比 ,则首项
,则首项 的最大值是 .
的最大值是 .
设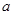 为大于
为大于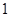 的常数,函数
的常数,函数 ,若关于
,若关于 的方程
的方程 恰有三个不同的实数解,则实数
恰有三个不同的实数解,则实数 的取值范围是 .
的取值范围是 .
如图,点 ,
, , ,
, , 分别是四面体的顶点或其棱的中点,则在同一平面内的四点组
分别是四面体的顶点或其棱的中点,则在同一平面内的四点组 (
(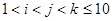 )共有 个.
)共有 个.
设 、
、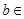 R,且
R,且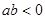 ,则( )
,则( )
A. |
B. |
C. |
D. |
“点 在曲线
在曲线 上”是“点
上”是“点 的坐标满足方程
的坐标满足方程 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
要得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
若在边长为 的正三角形
的正三角形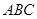 的边
的边 上有
上有 (
( N*,
N*, )等分点,沿向量
)等分点,沿向量 的方向依次为
的方向依次为 ,记
,记 ,若给出四个数值:①
,若给出四个数值:① ②
② ③
③ ④
④ ,则
,则 的值不可能的共有( )
的值不可能的共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 是椭圆
是椭圆 上的一点,求
上的一点,求 到
到 (
( )的距离的最小值.
)的距离的最小值.
已知函数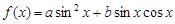 满足
满足
(1)求实数 的值以及函数
的值以及函数 的最小正周期;
的最小正周期;
(2)记 ,若函数
,若函数 是偶函数,求实数
是偶函数,求实数 的值.
的值.
如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm).(加工中不计损失).

(1)若钉身长度是钉帽高度的2倍,求铆钉的表面积;
(2)若每块钢板的厚度为 mm,求钉身的长度(结果精确到
mm,求钉身的长度(结果精确到 mm).
mm).
已知数列 的前
的前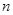 项和为
项和为 ,且
,且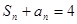 ,
, N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知 (
( N*),记
N*),记
 (
( 且
且 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列 是常数列,若存在,求出
是常数列,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列 ,对于任意的正整数
,对于任意的正整数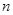 ,均有
,均有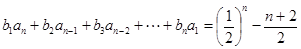 成立,求证:数列
成立,求证:数列 是等差数列;
是等差数列;
已知函数 ,若在定义域内存在
,若在定义域内存在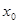 ,使得
,使得 成立,则称
成立,则称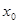 为函数
为函数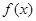 的局部对称点.
的局部对称点.
(1)若 、
、 R且
R且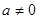 ,证明:函数
,证明:函数 必有局部对称点;
必有局部对称点;
(2)若函数 在区间
在区间 内有局部对称点,求实数
内有局部对称点,求实数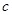 的取值范围;
的取值范围;
(3)若函数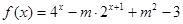 在R上有局部对称点,求实数
在R上有局部对称点,求实数 的取值范围.
的取值范围.