已知全集 ,集合
,集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
| A.(0,1) | B.(0,-1) | C.(-1,0) | D.(1,0) |
函数 的图象 ( )
的图象 ( )
A.关于 轴对称 轴对称 |
B.关于 轴对称 轴对称 |
| C.关于原点对称 | D.关于直线 对称 对称 |
给出下列三个命题:
①命题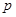 :
: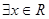 ,使得
,使得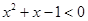 , 则
, 则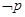 :
: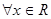 ,使得
,使得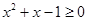
② 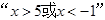 是“
是“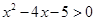 ”的充要条件.
”的充要条件.
③若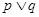 为真命题,则
为真命题,则 为真命题.
为真命题.
其中正确命题的个数为 ( )
| A.0 | B.1 | C. 2 | D.3 |
执行如图所示的程序框图,输出的 值是 ()
值是 ()
| A.2 | B.4 | C.8 | D.16 |
已知 则
则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知单位向量 和
和 的夹角为
的夹角为 ,记
,记 ,
,  , 则向量
, 则向量 与
与 的夹角为 ( )
的夹角为 ( )
A. |
B. |
C. |
D. |
一个三棱柱的侧视图、俯视图如图所示,则三棱柱的表面积是()
A. |
B. |
C. |
D. |
在平面直角坐标系中,椭圆 的焦距为
的焦距为 ,以
,以 为圆心,
为圆心, 为半径作圆,过点
为半径作圆,过点 作圆的两条切线互相垂直,则离心率
作圆的两条切线互相垂直,则离心率 为 ( )
为 ( )
A. |
B. |
C. |
D. |
设函数 ,若存在唯一的
,若存在唯一的 ,满足
,满足 ,则正实数
,则正实数 的最小值是 ( )
的最小值是 ( )
A. |
B. |
C. |
D. |
已知 是虚数单位,则
是虚数单位,则 .
.
函数 的图像在点
的图像在点 处的切线方程为 .
处的切线方程为 .
在 中,内角
中,内角 所对的边分别为
所对的边分别为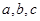 ,且满足
,且满足 ,则角B的大小为 .
,则角B的大小为 .
如图是一容量为 的样本的重量频率分布直方图,则由图可估计样本重量的中位数为 .
的样本的重量频率分布直方图,则由图可估计样本重量的中位数为 .

对于函数 ,有下列4个结论:
,有下列4个结论:
①任取 ,都有
,都有 恒成立;
恒成立;
②
 ,对于一切
,对于一切 恒成立;
恒成立;
③函数 有
有 个零点;
个零点;
④对任意 ,不等式
,不等式 恒成立.
恒成立.
则其中所有正确结论的序号是 .
已知函数 ,且周期为
,且周期为 .
.
(1)求 的值;
的值;
(2)当 [
[ ]时,求
]时,求 的最大值及取得最大值时
的最大值及取得最大值时 的值.
的值.
某校从高中部年满16周岁的学生中随机抽取来自高二和高三学生各10名,测量他们的身高,数据如下(单位:cm)
高二:166,158,170,169,180,171,176,175,162,163
高三:157,183,166,179,173,169,163,171,175,178
(1)若将样本频率视为总体的概率,从样本中来自高二且身高不低于170的学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率;
(2)根据抽测结果补充完整下列茎叶图,并根据茎叶图对来自高二和高三学生的身高作比较,写出两个统计结论.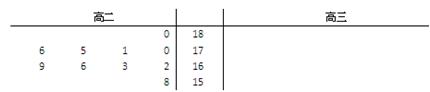
如图,一简单几何体的一个面 内接于圆
内接于圆 ,
, 分别是
分别是 的中点,
的中点, 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,且
为平行四边形,且 平面
平面 .
.
(1)求证: ∥平面
∥平面 ;
;
(2)若 ,
, ,试求该几何体的V.
,试求该几何体的V.
已知数列 是等差数列,首项
是等差数列,首项 ,公差为
,公差为 ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数 在
在 处取得极值
处取得极值 .
.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围.
的取值范围.
已知焦点在 轴上的椭圆
轴上的椭圆 ,焦距为
,焦距为 ,长轴长为
,长轴长为 .
.
(1)求椭圆的标准方程;
(2)过点 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于 两点.
两点.
①证明:点 到直线
到直线 的距离为定值,并求出这个定值;
的距离为定值,并求出这个定值;
②求 .
.