已知向量
，
，若
，则
（ ）
A． |
B． |
C． |
D． |
已知
是实数，则“
”是 “
” 的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分又不必要条件 |
函数
的零点所在的一个区间是（ ）．
| A．（－2，－1） | B．（－1,0） | C．（0,1） | D．（1,2） |
数列{a
}为等差数列，若a
＋a
＝
，则
的值为（ ）
A． |
B． |
C． |
D． |
的值为（ ）
A． |
B． |
C． |
D． |
已知函数
若
，则
的值为（ ）
A． |
B． |
| C．或 |
D． 或 |
已知
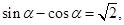
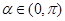，则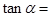
（ ）
| A．1 | B．-1 | C． |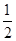
D． |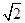
要得到函数
的图象，可由函数
的图像（ ）
A．向左平移 个长度单位 |
B．向右平移个长度单位 |
C．向左平移 个长度单位 |
D．向右平移个长度单位 |
在
中，
分别为
的对边，若
、
、
依次成等比数列，则（ ）
| A．依次成等差数列 |
B．依次成等比数列 |
C． 依次成等差数列 |
D．依次成等比数列 |
若函数
，
的最小正周期为
，且
，则（ ）．
A． ， |
B．， |
C． ， |
D．，． |
已知集合A=
，B=
，则
．
已知实数
满足等式
,给出下列五个关系式：
①
；②
；③
；④
；⑤
．
其中可能关系式是 ．
在△ABC中，角A，B，C所对的边分别是a，b， c，若
，
，则△ABC的面积等于 ．
等比数列
中，
,则
= ．
在平面直角坐标系中，
分别是与
轴正方向同向的单位向量，平面内三点
、
、
满足
，
，
，则实数m的值为 ．
平面向量
满足
，
，
，
，则
的最小值为 ．
已知
是以
为周期的偶函数，当
时，
，那么在区间
内，关于
的方程
（
且
）有
个不同的根，则
的取值范围是 ．
已知
是递增的等差数列，
（1）求数列的通项公式；
（2）若
，求数列
的前n项和
．
在
中，
分别为
的对边,已知
．
（1）求
；
（2）当
，
时，求的面积．
已知函数
，
．
（1）当
时，求函数
的最小值；
（2）若对任意 ，
恒成立，试求实数
的取值范围．
已知
，
，
（1）求函数
的单调增区间；
（2）当
时，求函数的值域．
已知定义域为
的奇函数
．
（1）解不等式
；
（2）对任意
，总有
，求实数
的取值范围．