已知i为虚数单位,复数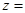
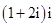 对应的点位于( )
对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
命题“若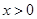 ,则
,则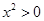 ”的否命题是( )
”的否命题是( )
A.若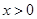 ,则 ,则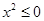 |
B.若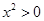 ,则 ,则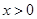 |
C.若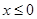 ,则 ,则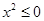 |
D.若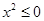 ,则 ,则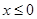 |
设向量 ,
, ,
, ,则实数
,则实数 的值是( )
的值是( )
A. |
B. |
C. |
D. |
函数 的最小正周期为( )
的最小正周期为( )
A. |
B. |
C. |
D. |
一算法的程序框图如图,若输出的 ,则输入的
,则输入的 的值可能为( )
的值可能为( )
A. |
B. |
C. |
D. |
用 ,
, ,
, 表示空间中三条不同的直线,
表示空间中三条不同的直线,  表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若 ,
,  , 则
, 则 ∥
∥ ; ② 若
; ② 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ;
;
③ 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ; ④ 若
; ④ 若

 ,
, 

 , 则
, 则 ∥
∥ .
.
其中真命题的序号是( )
| A.①② | B.②③ | C.①④ | D.②④ |
已知 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. |
B. |
C. |
D. |
已知双曲线 的左,右焦点分别为
的左,右焦点分别为 ,
, ,过点
,过点 的直线与双曲线
的直线与双曲线 的右支相交于
的右支相交于 ,
, 两点,且点
两点,且点 的横坐标为
的横坐标为 ,则△
,则△ 的周长为( )
的周长为( )
A. |
B. |
C. |
D. |
已知函数 , 则
, 则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
不等式 的解集是 .
的解集是 .
在平面直角坐标系 中,设不等式组
中,设不等式组 所表示的平面区域是
所表示的平面区域是 ,从区域
,从区域 中随机取点
中随机取点 ,则
,则 的概率是 .
的概率是 .
已知实数 ,
, 满足
满足 ,则
,则 的最大值为 .
的最大值为 .
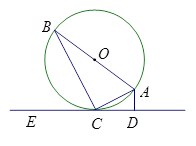
(几何证明选讲选做题)如图,圆 的直径
的直径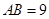 ,直线
,直线 与圆
与圆 相切于点
相切于点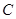 ,
, 于点D,若
于点D,若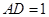 ,设
,设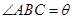 ,则
,则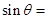 ______.
______.
(坐标系与参数方程选讲选做题)在极坐标系中,设曲线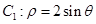 与
与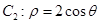 的交点分别为
的交点分别为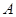 ,
,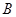 ,则线段
,则线段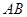 的垂直平分线的极坐标方程为 .
的垂直平分线的极坐标方程为 .
(本小题满分12分)
已知函数
 R
R ,
, 是函数
是函数 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数 的单调递增区间;
的单调递增区间;
(2)若
 ,且
,且 ,
, ,求
,求 的值.
的值.
(本小题满分12分)
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量 (杯),得到如下数据:
(杯),得到如下数据:
| 日 期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量 (杯) (杯) |
23 |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程 .
.
(参考公式: .)
.)
(本小题满分14分)
如图,在多面体 中,
中, 平面
平面 ,
, ∥
∥ ,平面
,平面 平面
平面
 ,
, ,
, ,
, .
.
(1)求证: ∥
∥ ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分14分)
已知首项为 ,公比不等于
,公比不等于 的等比数列
的等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
 .
.
(本小题满分14分)
已知椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 .圆
.圆 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线
 与椭圆C有且只有一个公共点
与椭圆C有且只有一个公共点 ,且
,且 与圆
与圆 相交于
相交于 两点,问
两点,问
 是否成立?请说明理由.
是否成立?请说明理由.
(本小题满分14分)
已知函数 在点
在点 处的切线为
处的切线为 .
.
(1)求实数 ,
, 的值;
的值;
(2)是否存在实数 ,当
,当 时,函数
时,函数 的最小值为
的最小值为 ,若存在,求出
,若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若 ,求证:
,求证: .
.