已知集合 ,
,
A.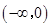 |
B. |
C. |
D. |
若复数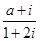 是纯虚数,则实数
是纯虚数,则实数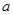 的值为
的值为
A.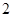 |
B. |
C.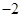 |
D. |
圆 和圆
和圆 的位置关系为
的位置关系为
| A.相交 | B.相切 | C.相离 | D.以上都有可能 |
已知函数 ,则函数
,则函数 的大致图象为
的大致图象为
下列命题:
①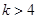 是方程
是方程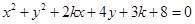 表示圆的充要条件;
表示圆的充要条件;
②把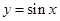 的图象向右平移
的图象向右平移 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的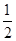 ,得到函数
,得到函数 的图象;
的图象;
③函数 上为增函数;
上为增函数;
④椭圆 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5.
其中正确命题的序号为
| A.①③④ | B.②③④ | C.②④ | D.② |
一个几何体的的三视图如右图所示,则该几何体的体积为
| A.2 | B. |
C.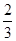 |
D. |
如果执行如图的程序框图,那么输出的值是
| A.2016 | B.2 | C. |
D. |
函数 的零点所在的大致区间是
的零点所在的大致区间是
A. |
B. |
C. |
D. |
已知 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为
的大小关系为
A. |
B. |
C. |
D. |
设非负实数 满足
满足 ,则
,则 的最大值为_______.
的最大值为_______.
观察式子 则可归纳出关于正整数
则可归纳出关于正整数 的式子为__________________.
的式子为__________________.
椭圆 与双曲线
与双曲线 有公共的焦点
有公共的焦点 ,则双曲线的渐近线方程为________.
,则双曲线的渐近线方程为________.
若平面向量 ,则
,则 的实数
的实数 的集合为___.
的集合为___.
 在
在 上恒为单调递增函数,则实数
上恒为单调递增函数,则实数 的取值范围________.
的取值范围________.
(本小题满分12分)
已知直线两直线 中,内角A,B,C对边分别为
中,内角A,B,C对边分别为 时,两直线恰好相互垂直;
时,两直线恰好相互垂直;
(I)求A值;
(II)求b和 的面积
的面积
(本小题满分12分)
右图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人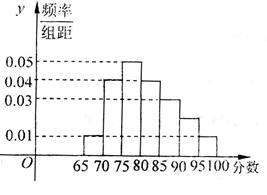
(I)求该专业毕业总人数N和90~95分数段内的人数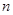 ;
;
(II)现欲将90~95分数段内的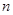 名人分配到几所学校,从中安排2人到甲学校去,若
名人分配到几所学校,从中安排2人到甲学校去,若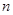 人中仅有两名男生,求安排结果至少有一名男生的概率.
人中仅有两名男生,求安排结果至少有一名男生的概率.
(本小题满分12分)
如图,ABCD为梯形,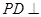 平面ABCD,AB//CD,
平面ABCD,AB//CD,
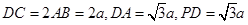 ,E为BC中点
,E为BC中点
(I)求证:平面 平面PDE;
平面PDE;
(II)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
(本小题满分12分)
已知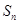 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列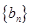 是等比数列,
是等比数列,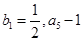 恰为
恰为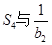 的等比中项,圆
的等比中项,圆 ,直线
,直线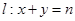 ,对任意
,对任意 ,直线
,直线 都与圆C相切.
都与圆C相切.
(I)求数列 的通项公式;
的通项公式;
(II)若对任意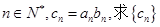 的前n项和
的前n项和 的值.
的值.
(本小题满分13分)
已知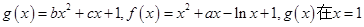 处的切线为
处的切线为
(I)求 的值;
的值;
(II)若 的极值;
的极值;
(III)设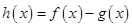 ,是否存在实数
,是否存在实数 (
( ,为自然常数)时,函数
,为自然常数)时,函数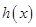 的最小值为3.
的最小值为3.
(本小题满分14分)
已知抛物线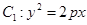 上一点
上一点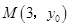 到其焦点F的距离为4;椭圆
到其焦点F的距离为4;椭圆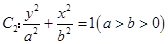 的离心率
的离心率 ,且过抛物线的焦点F.
,且过抛物线的焦点F.
(I)求抛物线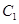 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点F的直线 交抛物线
交抛物线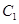 于A、B两不同点,交
于A、B两不同点,交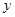 轴于点N,已知
轴于点N,已知 ,求证:
,求证: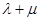 为定值.
为定值.
(III)直线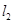 交椭圆
交椭圆 于P,Q两不同点,P,Q在x轴的射影分别为
于P,Q两不同点,P,Q在x轴的射影分别为 ,
, ,
,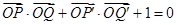 ,若点S满足:
,若点S满足: ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.