已知i是虚数单位.若复数z满足 ,则复数z=
,则复数z=
A. |
B. |
C. |
D. |
设全集为R,集合 ,则
,则
A. |
B. |
C. |
D. |
已知函数 ,则
,则 的值为
的值为
A. |
B.0 | C.1 | D.2 |
已知 为第二象限角,
为第二象限角, ,则
,则 的值等于
的值等于
A. |
B. |
C. |
D. |
已知 ,则向量
,则向量 的夹角为
的夹角为
A. |
B. |
C. |
D. |
某程序框图如图所示,当输出y值为 时,则输出x的值为
时,则输出x的值为
| A.64 | B.32 |
| C.16 | D.8 |
设 是q的
是q的
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
函数 的大致图象为
的大致图象为
已知函数 ,则函数
,则函数 的零点所在的区间是
的零点所在的区间是
A. |
B. |
C. |
D. |
已知 是双曲线
是双曲线 的左右两个焦点,过点
的左右两个焦点,过点 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段
与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段 为直径的圆外,则该双曲线离心率的取值范围是
为直径的圆外,则该双曲线离心率的取值范围是
A. |
B. |
C. |
D. |
一个容量为n的样本,分成若干组,已知某组的频数和频率分别为30和0.25,则n等于_________.
一个正四棱锥的侧棱长与底面边长相等,体积为 ,则它的表面积为________.
,则它的表面积为________.
设实数 满足
满足 ,则
,则 的最大值是________.
的最大值是________.
已知直线 和圆
和圆 相交于A,B两点,当线段AB最短时直线l的方程为________.
相交于A,B两点,当线段AB最短时直线l的方程为________.
在平面直角坐标系中,O为坐标原点,A(1,0),B(0,3),C(3,0),动点D满足 ,则
,则 的最小值是__________.
的最小值是__________.
某省为了研究雾霾天气的治理,一课题组对省内24个城市进行了空气质量的调查,按地域特点把这些城市分成了甲、乙、丙三组.已知三组城市的个数分别为4,8,12,课题组用分层抽样的方法从中抽取6个城市进行空气质量的调查.
(I)求每组中抽取的城市的个数;
(II)从已抽取的6个城市中任抽两个城市,求两个城市不来自同一组的概率.
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(II)将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象.在
的图象.在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,若
,若 ,求
,求 的面积.
的面积.
如图,在三棱柱 中,四边形
中,四边形 都为矩形.
都为矩形.
(I)设D是AB的中点,证明:直线 平面
平面 ;
;
(II)在 中,若
中,若 ,证明:直线
,证明:直线 平面
平面 .
.
已知等差数列 的前n项和为
的前n项和为 ,满足
,满足 ,
, 为递增的等比数列,且
为递增的等比数列,且 是方程
是方程 的两个根.
的两个根.
(I)求数列 ,
, 的通项公式;
的通项公式;
(II)若数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和 .
.
已知椭圆 的离心率
的离心率 ,直线
,直线 经过椭圆C的左焦点.
经过椭圆C的左焦点.
(I)求椭圆C的方程;
(II)若过点 的直线与椭圆C交于A,B两点,设P为椭圆上一点,且满足
的直线与椭圆C交于A,B两点,设P为椭圆上一点,且满足 (其中O为坐标原点),求实数t的取值范围.
(其中O为坐标原点),求实数t的取值范围.
函数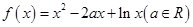 .
.
(I)函数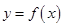 在点
在点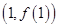 处的切线与直线
处的切线与直线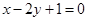 垂直,求a的值;
垂直,求a的值;
(II)讨论函数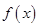 的单调性;
的单调性;
(III)不等式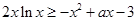 在区间
在区间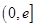 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.