函数y=sin2xcos2x的最小正周期是 .
若集合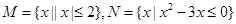 ,则M∩N
,则M∩N .
.
复数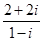 = .(
= .(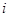 是虚数单位)
是虚数单位)
已知数列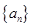 的前
的前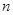 项和
项和 ,则其通项公式为
,则其通项公式为
已知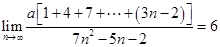 ,则
,则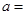
已知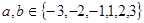 且
且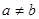 ,则复数
,则复数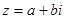 对应点在第二象限的概率为 .(用最简分数表示)
对应点在第二象限的概率为 .(用最简分数表示)
已知函数 ,
,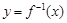 是函数
是函数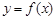 的反函数,若
的反函数,若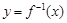 的图象过点
的图象过点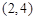 ,则
,则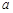 的值为 .
的值为 .
如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是______________.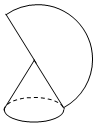
根据下面的框图,打印的最后一个数据是______________.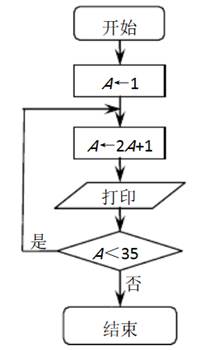
已知数列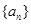 是以
是以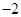 为公差的等差数列,
为公差的等差数列,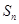 是其前
是其前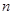 项和,若
项和,若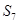 是数列
是数列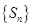 中的唯一最大项,则数列
中的唯一最大项,则数列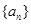 的首项
的首项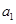 的取值范围是 .
的取值范围是 .
五位同学各自制作了一张贺卡,分别装入5个空白信封内,这五位同学每人随机地抽取一封,则恰好有两人抽取到的贺卡是其本人制作的概率是 .
已知△ABC中,角A、B、C的对边分别为a、b、c,且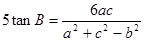 , 则
, 则 的值是 .
的值是 .
如图,在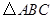 中,点
中,点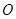 是
是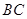 的中点,过点
的中点,过点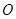 的直线分别交直线
的直线分别交直线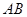 ,
, 于不同的两点
于不同的两点 ,若
,若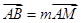 ,
, ,则
,则 的值为 .
的值为 .
已知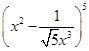 的展开式中的常数项为
的展开式中的常数项为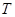 ,
,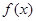 是以
是以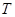 为周期的偶函数,且当
为周期的偶函数,且当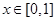 时,
时,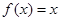 ,若在区间
,若在区间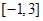 内,函数
内,函数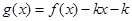 有4个零点,则实数
有4个零点,则实数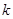 的取值范围是 .
的取值范围是 .
设z1、z2∈C,则“z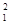 +z
+z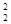 =0”是“z1=z2=0”的 ( )
=0”是“z1=z2=0”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若正数a,b,c成公差不为零的等差数列,则 ( )
A. 成等差数列 成等差数列 |
B. 成等比数列 成等比数列 |
C.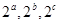 成等差数列 成等差数列 |
D.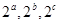 成等比数列 成等比数列 |
函数 的图象为( )
的图象为( )
A. |
B. |
C. |
D.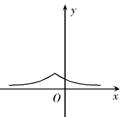 |
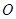 是△ABC所在平面内的一点,且满足
是△ABC所在平面内的一点,且满足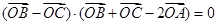 ,则△ABC的形状一定是( )
,则△ABC的形状一定是( )
| A.正三角形 | B.直角三角形 | C.等腰三角形 | D.斜三角形 |
如图:三棱锥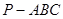 中,
中, ^底面
^底面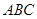 ,若底面
,若底面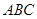 是边长为2的正三角形,且
是边长为2的正三角形,且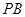 与底面
与底面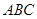 所成的角为
所成的角为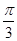 .若
.若 是
是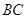 的中点,求:
的中点,求:
(1)三棱锥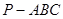 的体积;
的体积;
(2)异面直线 与
与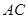 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).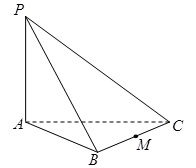
已知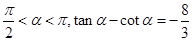
(1)求 的值;
的值;
(2)求 的值.
的值.
已知数列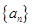 为等差数列,公差
为等差数列,公差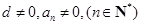 ,且
,且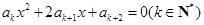
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为 …,求证:数列
…,求证:数列 为等差数列.
为等差数列.
已知函数 ,
, .
.
(1)证明:函数 在区间
在区间 上为增函数,并指出函数
上为增函数,并指出函数 在区间
在区间 上的单调性.
上的单调性.
(2)若函数 的图像与直线
的图像与直线 有两个不同的交点
有两个不同的交点 ,
, ,其中
,其中 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
(3)求 的取值范围.
的取值范围.
对于给定数列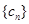 ,如果存在实常数
,如果存在实常数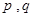 使得
使得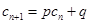 对于任意
对于任意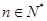 都成立,我们称数列
都成立,我们称数列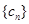 是 “线性数列”.
是 “线性数列”.
(1)若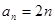 ,
,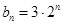 ,
,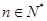 ,数列
,数列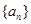 、
、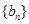 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列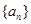 是“线性数列”,则数列
是“线性数列”,则数列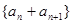 也是“线性数列”;
也是“线性数列”;
(3)若数列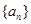 满足
满足 ,
, ,
,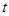 为常数.求数列
为常数.求数列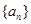 前
前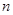 项的和.
项的和.