函数 的周期是 .
的周期是 .
计算 = .
= .
计算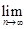
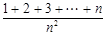 = .
= .
二项式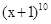 展开式中,
展开式中,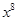 的系数为 .
的系数为 .
设矩阵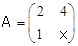 ,
,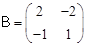 ,若
,若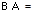
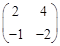 ,则
,则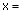 .
.
现有6位同学排成一排照相,其中甲、乙二人相邻的排法有 种.
若 ,
, ,则
,则 .
.
若一个球的体积为 ,则它的表面积为__________.
,则它的表面积为__________.
若函数 是
是 上的偶函数,则
上的偶函数,则 的值是 .
的值是 .
正四棱锥 的所有棱长均相等,
的所有棱长均相等, 是
是 的中点,那么异面直线
的中点,那么异面直线 与
与 所成的角的余弦值等于 .
所成的角的余弦值等于 . 
直线 被曲线
被曲线
 所截得的弦长等于 .
所截得的弦长等于 .
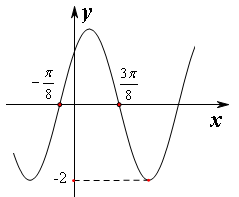
已知函数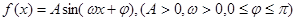 的部分图像如图所示,则
的部分图像如图所示,则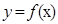 的解析式是
的解析式是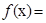 .
.
已知点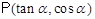 在第三象限,则角
在第三象限,则角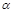 的终边在( )
的终边在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知函数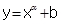 ,
,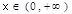 是增函数,则 ( )
是增函数,则 ( )
A.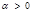 , ,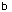 是任意实数 是任意实数 |
B.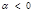 , ,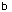 是任意实数 是任意实数 |
C.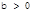 , ,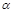 是任意实数 是任意实数 |
D.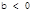 , ,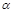 是任意实数 是任意实数 |
在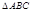 中,若
中,若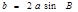 ,则这个三角形中角
,则这个三角形中角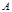 的值是( )
的值是( )
A. 或 或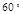 |
B.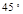 或 或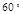 |
C.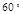 或 或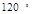 |
D. 或 或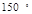 |
若 ,则( )
,则( )
A. |
B. |
C. |
D. |
双曲线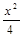 -
-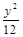 =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( )
A.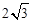 |
B.2 | C.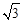 |
D.1 |
用数学归纳法证明等式 (n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到( )
(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到( )
A. |
B. |
C. |
D. |
设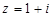 (
(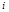 是虚数单位),则复数
是虚数单位),则复数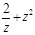 对应的点位于( )
对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
圆 在点
在点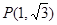 处的切线方程为 ( )
处的切线方程为 ( )
A. |
B.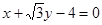 |
C.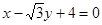 |
D.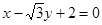 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
在四边形ABCD中, ,
, ,则四边形的面积为( )
,则四边形的面积为( )
A. |
B. |
C.5 | D.10 |
函数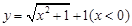 的反函数是( )
的反函数是( )
A.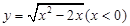 |
B.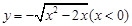 |
C.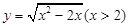 |
D.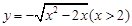 |
曲线 的部分图像是( )
的部分图像是( )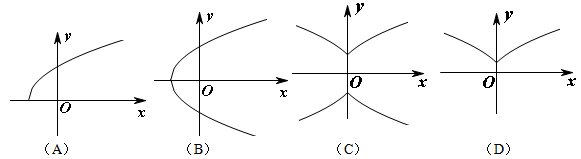
(本题满分 8 分)解不等式组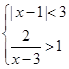
(本题满分 8 分)如图,正四棱柱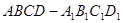 的底面边长
的底面边长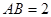 ,若异面直线
,若异面直线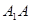 与
与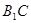 所成角的大小为
所成角的大小为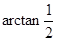 ,求正四棱柱
,求正四棱柱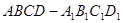 的体积.
的体积.
(本题满分 10 分)本题共有 2 个小题,第 1 小题满分 4 分,第 2 小题满分6分.
已知点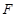 为抛物线
为抛物线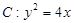 的焦点,点
的焦点,点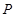 是准线
是准线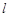 上的动点,直线
上的动点,直线 交抛物线
交抛物线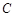 于
于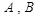 两点,若点
两点,若点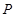 的纵坐标为
的纵坐标为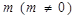 ,点
,点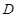 为准线
为准线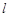 与
与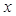 轴的交点.
轴的交点.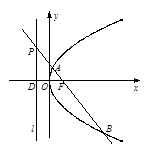
(1)求直线 的方程;
的方程;
(2)求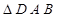 面积
面积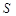 的取值范围.
的取值范围.
(本题满分 10 分)本题共有 2 个小题,第 1 小题满分 4 分,第 2 小题满分6分.
已知函数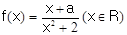 .
.
(1)写出函数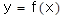 的奇偶性;
的奇偶性;
(2)当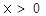 时,是否存实数
时,是否存实数 ,使
,使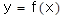 的图像在函数
的图像在函数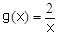 图像的下方,若存在,求
图像的下方,若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
本题共有 3 个小题,第 1 小题满分 3 分,第 2 小题满分4分,第 3 小题满分5分.
已知抛物线 ,过原点作斜率为1的直线交抛物线于第一象限内一点
,过原点作斜率为1的直线交抛物线于第一象限内一点 ,又过点
,又过点 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点 ,再过
,再过 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点 ,
, ,如此继续。一般地,过点
,如此继续。一般地,过点 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点 ,设点
,设点 .
.
(1)求 的值;
的值;
(2)令 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(3)记 为点列
为点列 的极限点,求点
的极限点,求点 的坐标.
的坐标.
(本题满分 8 分)有根木料长为6米,要做一个如图的窗框,已知上框架与下框架的高的比为1∶2,问怎样利用木料,才能使光线通过的窗框面积最大(中间木档的面积可忽略不计).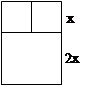
(本题满分 10 分)本题共有 2 个小题,第 1 小题满分 4 分,第 2 小题满分6分.
在平面直角坐标系 中,点
中,点 到两点
到两点 、
、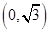 的距离之和等于4.设点
的距离之和等于4.设点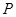 的轨迹为
的轨迹为 .
.
(1)写出轨迹 的方程;
的方程;
(2)设直线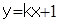 与
与 交于
交于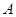 、
、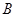 两点,问
两点,问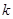 为何值时
为何值时 此时|
此时|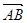 |的值是多少?
|的值是多少?
(本题满分 12 分)本题共有 3 个小题,第 1 小题满分 3分,第 2 小题满分 4分,第 3小题满分5 分.
设数列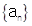 的首项
的首项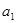 为常数,且
为常数,且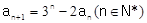 .
.
(1)证明: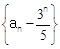 是等比数列;
是等比数列;
(2)若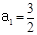 ,
,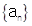 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若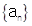 是递增数列,求
是递增数列,求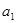 的取值范围.
的取值范围.