集合 ,则
,则 ( ).
( ).
A. |
B. |
C. |
D. |
设 ,则
,则 是
是 的( ).
的( ).
| A.充要条件 |
| B.充分但不必要条件 |
| C.必要但不充分条件 |
| D.既不充分也不必要条件 |
已知函数 是偶函数,且
是偶函数,且 ,则
,则 ( ).
( ).
| A.-3 | B.-1 | C.1 | D.2 |
 的展开式的常数项是( ).
的展开式的常数项是( ).
| A.2 | B.3 | C.-2 | D.-3 |
如下图,在△OAB中,P为线段AB上的一点, =x
=x +y
+y ,且
,且 =3
=3 ,则( ).
,则( ).
A.x= ,y= ,y= |
B.x= ,y= ,y= |
C.x= ,y= ,y= |
D.x= ,y= ,y= |
定义运算 为执行如图所示的程序框图输出的S值,则
为执行如图所示的程序框图输出的S值,则
 的值为( ).
的值为( ).
| A.2 | B.-2 | C.-1 | D.1 |
已知最小正周期为2的函数 在区间
在区间 上的解析式是
上的解析式是 ,则函数
,则函数 在实数集R上的图象与函数
在实数集R上的图象与函数 的图象的交点的个数是 ( ).
的图象的交点的个数是 ( ).
| A.3 | B.4 | C.5 | D.6 |
已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( ).

如图,矩形ABCD的四个顶点的坐标分别为A(0,—1),B( ,—1),C(
,—1),C( ,1),D(0,1),正弦曲线
,1),D(0,1),正弦曲线 和余弦曲线
和余弦曲线 在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).
在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).
A. |
B. |
C. |
D. |
若数列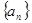 满足:存在正整数
满足:存在正整数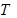 ,对于任意正整数
,对于任意正整数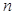 都有
都有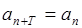 成立,则称数列
成立,则称数列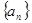 为周期数列,周期为
为周期数列,周期为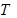 .已知数列
.已知数列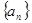 满足
满足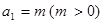 ,
, 则下列结论中错误的是( ).
则下列结论中错误的是( ).
A.若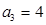 ,则 ,则 可以取3个不同的值; 可以取3个不同的值; |
B.若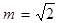 ,则数列 ,则数列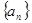 是周期为3的数列; 是周期为3的数列; |
C. 且 且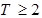 ,存在 ,存在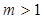 ,数列 ,数列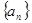 周期为 周期为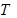 ; ; |
D.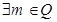 且 且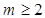 ,数列 ,数列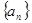 是周期数列. 是周期数列. |
在直角坐标系xOy中,直线 的参数方程为
的参数方程为 (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ,则直线
,则直线 和曲线C的公共点有 个.
和曲线C的公共点有 个.
如图,圆O的直径AB = 8,C为圆周上一点,BC = 4,过C作圆的切线 ,过A作直线
,过A作直线 的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .
的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .
若 ,则
,则 的最小值为________.
的最小值为________.
设实数 满足
满足 ,向量
,向量 .若
.若 ,则实数m的最小值为 .
,则实数m的最小值为 .
已知两定点A(-1,0)和B(1,0),动点 在直线
在直线 上移动,椭圆C
上移动,椭圆C
以A,B为焦点且经过点P,则椭圆C的离心率的最大值为 .
若函数 在定义域内给定区间[a,b]上存在
在定义域内给定区间[a,b]上存在 ,满足
,满足 ,则称函数
,则称函数 是[a,b]上的“平均值函数”,
是[a,b]上的“平均值函数”,  是它的一个均值点.例如
是它的一个均值点.例如 是[-2,2]上的“平均值函数”,O就是它的均值点.若函数
是[-2,2]上的“平均值函数”,O就是它的均值点.若函数 是[-1,1]上的“平均值函数”,则实数
是[-1,1]上的“平均值函数”,则实数 的取值范围是 .
的取值范围是 .
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求 的分布列和均值(数学期望).
的分布列和均值(数学期望).
(本小题满分12分)如图,摩天轮上一点 在
在 时刻距离地面高度满足
时刻距离地面高度满足
 ,已知某摩天轮的半径为
,已知某摩天轮的半径为 米,点
米,点 距地面的高度为
距地面的高度为 米,摩天轮做匀速转动,每
米,摩天轮做匀速转动,每 分钟转一圈,点
分钟转一圈,点 的起始位置在摩天轮的最低点处.
的起始位置在摩天轮的最低点处.
(1)根据条件写出 (米)关于
(米)关于 (分钟)的解析式;
(分钟)的解析式;
(2)在摩天轮转动的一圈内,有多长时间点 距离地面超过
距离地面超过 米?
米?
(本小题满分12分)如图,在四棱锥 中,
中, ,四边形
,四边形 是菱形,
是菱形,
 且
且 交于点
交于点 ,
, 是
是 上任意一点.
上任意一点.
(1)求证: ;
;
(2)已知二面角 的余弦值为
的余弦值为 ,若
,若 为
为 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分13分)为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换10000辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车 辆,混合动力型公交车
辆,混合动力型公交车 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入 辆.设
辆.设 、
、 分别为第
分别为第 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设 、
、 分别为
分别为 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求 、
、 ,并求
,并求 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数 ;
;
(2)该市计划用 年的时间完成全部更换,求
年的时间完成全部更换,求 的最小值.
的最小值.
(本小题满分13分)如图,已知圆E: ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点,直线
两点,直线 的斜率分别为
的斜率分别为 (其中
(其中 ).△
).△ 的面积为
的面积为 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列, 求
恰好构成等比数列, 求 的取值范围.
的取值范围.
(本小题满分13分)已知 .
.
(1)若 ,函数
,函数 在其定义域内是增函数,求
在其定义域内是增函数,求 的取值范围;
的取值范围;
(2) 的图象与
的图象与 轴交于
轴交于 )两点,
)两点, 中点为
中点为 ,求证:
,求证: .
.