复数
，则
的模为( )．
A． |
B． |
C． |
D． |
函数
的定义域是( )．
A． |
B． |
C． |
D． |
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4．0 |
2．5 |
 0．5 |
0．5 |
2．0 |
得到的回归方程为
．若
，则
每增加1个单位，
就( )．
A．增加
个单位 B．减少个单位
C．增加
个单位 D．减少个单位
“
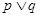为真命题”是“
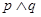为真命题”的( )．
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．非充分非必要条件 |
将函数
的图象向右平移
个单位，然后纵坐标不变横坐标伸长为原来的2倍，得到函数解析式为( )．
A． |
B． |
C． |
D． |
已知
是圆
：
内一点，现有以
为中点的弦所在
直线
和直线
：
，则( )．
A． ，且与圆相交 |
B． ，且与圆相交 |
| C．，且与圆相离 |
D．，且与圆相离 |
执行如图所示的程序框图，输出的x值为( )． 
| A．7 | B．6 | C．5 | D．4 |
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形（如图），则该棱锥的外接球的半径是( )．
A． |
B． |
C．2 | D． |
设a为大于1的常数，函数
若关于x的方程
恰有三个不同的实数解，则实数b的取值范围是( )．
| A．0＜b≤1 | B．0＜b＜1 | C．0≤b≤1 | D．b＞1． |
如图，正
的中心位于点G
，A
，动点P从A点出发沿的边界
按逆时针方向运动，设旋转的角度
，向量
在
方向的投影
为y（O为坐标原点），则y关于x的函数
的图像是( )．
设集合
，
，则集合
= ．
在极坐标系中，点
到直线
的距离是 ．
设实数
满足
，则目标函数
的最小值为 ．
如图，直线
与圆
及抛物线
依次交于A、B、C、D四点，则
．
若存在实数
，使得
，则实数
的取值范围是 ．
（本小题满分12分）已知数列
满足
=5，且其前
项和
．
（Ⅰ）求
的值和数列的通项公式；
（Ⅱ）设
为等比数列，公比为
，且其前项和
满足
，求
的取值范围．
（本小题满分12分）
某网站针对“2015年春节放假安排”开展网上问卷调查，提出了A，B两种放假方案，调查结果如下表（单位：万人）：
| 人群 |
青少年 |
中年人 |
老年人 |
| 支持A方案 |
200 |
400 |
800 |
| 支持B方案 |
100 |
100 |
 |
已知从所有参与调查的人中任选1人是“老年人”的概率为
．
（Ⅰ）求的值；
（Ⅱ）从参与调查的“老年人”中，用分层抽样的方法抽取6人，在这6人中任意选取2人，求恰好有1人“支持B方案”的概率．
（本小题满分12分）如图，四棱锥
中，
是正三角形，四边形
是矩形，且平面
平面，
，
．
（Ⅰ）若点
是
的中点，求证：
平面
；
（Ⅱ）若点
在线段
上，且
，当三棱锥
的体积为
时，求实数
的值．
(本小题满分13分)设函数
（Ⅰ）求
的最小正周期及值域；
（Ⅱ）已知
中，角
的对边分别为
，若
，
，
，求的面积．
（本小题满分13分）如图所示的“8”字形曲线是由两个关于
轴对称的半圆和一个双曲线的一部分组成的图形，其中上半个圆所在圆方程是
，双曲线的左、右顶点
、
是该圆与轴的交点，双曲线与半圆相交于与轴平行的直径的两端点．
（1）试求双曲线的标准方程；
（2）记双曲线的左、右焦点为
、
，试在“8”字形曲线上求点
，使得
是直角．
（本小题满分13分）已知函数
，其中
为常数，且
．
（1）若曲线
在点
处的切线与直线
垂直，求的值；
（2）若函数
在区间
上的最小值为
，求的值．