已知
，
，则
（ ）
A． |
B． |
C． |
D． |
把一个骰子连续抛掷两次，第一次得到的点数为
，第二次得到的点数为
，则事件“
”的概率为（ ）
A． |
B． |
C． |
D． |
抛物线
的准线方程是（ ）
A． |
B． |
C． |
D． |
某几何体的三视图如图所示，它的体积为（ ）
A． |
B． |
C． |
D． |
甲、乙两位同学在高二
次月考的数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是
、
，则下列正确的是（ ）
A． ，甲比乙成绩稳定 |
B． ，乙比甲成绩稳定 |
| C．，甲比乙成绩稳定 |
| D．，乙比甲成绩稳定 |
阅读如右图所示的程序框图，则该算法的功能是（ ）
A．计算数列 前 项的和 |
B．计算数列 前项的和 |
C．计算数列前 项的和 |
| D．计算数列前项的和 |
下列结论正确的是（ ）
A．命题“若 ，则 ”是真命题 |
B．若函数 可导，且在 处有极值，则 |
C．向量 ， 的夹角为钝角的充要条件是 |
D．命题 “ ， ”的否定是“ ， ” |
等差数列
的前
项和为
，
，
，则
（ ）
A． |
B． |
C． |
D． |
已知函数
满足对任意
，都有
成立，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
若两条异面直线所成的角为
，则称这对异面直线为“黄金异面直线对”，在连结正方体各顶点的所有直线中，“黄金异面直线对”共有（ ）
A． 对 |
B． 对 |
C． 对 |
D． 对 |
已知随机变量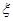
服从正态分布
，
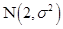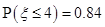，则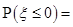
．
过双曲线
（
，
）的一个焦点
作一条渐近线的垂线，若垂足恰在线段
（
为坐标原点）的垂直平分线上，则双曲线的离心率为 ．
某老师从课本上抄录一个随机变量
的概率分布列如下表：
请甲同学计算的数学期望，尽管“
”处完全无法看清，且两个“
”处字迹模糊，但能断定这两个“”处的数值相同，据此，该同学给出了正确答案
．
在
中，内角
，
，
的对边分别为
，
，
，且满足
，则
．
已知定义在区间
上的函数
的图象如图所示，对于满足
的任意
，
，给出下列结论：
①
；
②
；
③
；
④
．
其中正确结论的序号是 ．（把所有正确结论的序号都填上）
（本小题满分13分）某同学用“五点法”画函数
在某一个周期的图象时，列表并填入的部分数据如下表：
（1）求
，
，
的值及函数
的表达式；
（2）将函数的图象向左平移
个单位，可得到函数
的图象，求函数
在区间
的最小值．
本小题满分13分）已知椭圆
（
）的右焦点与抛物线
的焦点重合，且椭圆
的离心率
．
（1）求椭圆的标准方程；
（2）若直线
（
）与椭圆交于不同的两点
，
，以线段
为直径作圆
．若圆与
轴相切，求直线
被圆所截得的弦长．
（本小题满分13分）我国东部某风景区内住着一个少数民族部落，该部落拟投资
万元用于修复和加强民俗文化基础设施．据测算，修复好部落民俗文化基础设施后，任何一个月（每月均按
天计算）中第
天的游客人数
近似满足
（单位：千人），第天游客人均消费金额
近似满足
（单位：元）．
（1）求该部落第天的日旅游收入
（单位：千元，
，
）的表达式；
（2）若以一个月中最低日旅游收入金额的
%作为每一天应回收的投资成本，试问该部落至少经过几年就可以收回全部投资成本．
（本小题满分13分）如图，在四棱锥
中，侧棱
底面
，
，
，
，
，
是棱
中点．
（1）求证：
平面
；
（2）设点
是线段
上一动点，且
，当直线
与平面
所成的角最大时，求
的值．
（本小题满分14分）已知函数
（
）．
（1）当
时，求函数
的图象在点
处的切线方程；
（2）设
，求证：当
时，
；
（3）若函数
恰有两个零点
，
（
），求实数
的取值范围．
（本小题满分7分）选修4-2：矩阵与变换
已知线性变换
把点
变成了点
，把点
变成了点
．
（1）求变换所对应的矩阵
；
（2）求直线
在变换的作用下所得到的直线方程．
（本小题满分7分）选修4-4：极坐标与参数方程
在平面直角坐标系中，以坐标原点为极点，
轴的正半轴为极轴建立极坐标系．已知直线
的极坐标方程为
（
为常数），圆
的参数方程为
（
为参数）．
（1）求直线的直角坐标方程和圆的普通方程；
（2）若圆心关于直线的对称点亦在圆上，求实数的值．
（本小题满分7分）选修4-5：不等式选讲
已知
（
，
，
）．
（1）求
的最小值；
（2）若
对满足条件的一切实数，，
恒成立，求实数
的取值范围．