 为虚数单位,则
为虚数单位,则 等于( )
等于( )
A. |
B. |
C. |
D. |
已知集合 ,
, ,若
,若 ,则
,则 为( )
为( )
A. |
B. |
C. |
D. |
函数 的零点个数为( )
的零点个数为( )
A. |
B. |
C. |
D. |
设 ,
, ,那么“
,那么“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
执行右边的程序框图,若 ,则输出的
,则输出的 为( )
为( )
A. |
B. |
C. |
D. |
已知向量 ,
, ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
已知两条不同直线 ,
, ,三个不同平面
,三个不同平面 ,
, ,
,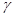 ,下列命题中正确是( )
,下列命题中正确是( )
A.若 , , ,则 ,则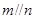 |
B.若 , ,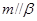 ,则 ,则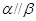 |
C.若 , ,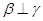 ,则 ,则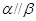 |
D.若 , , ,则 ,则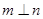 |
在一次歌咏比赛中,七位裁判为以选手打出的分数如下:






去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A. , , |
B. , , |
C. , , |
D. , , |
函数 在
在 上的图象是( )
上的图象是( )
同时具有性质:“①最小正周期是 ;②图象关于点
;②图象关于点 对称;③在
对称;③在 上是减函数”的一个函数是( )
上是减函数”的一个函数是( )
A. |
B. |
C. |
D. |
已知函数 ,若对于任意
,若对于任意 ,都有
,都有 成立,则实数
成立,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
过双曲线 (
( ,
, )的一个焦点
)的一个焦点 作一条渐近线的垂线,若垂足恰在线段
作一条渐近线的垂线,若垂足恰在线段 (
( 为坐标原点)的垂直平分线上,则双曲线的离心率为( )
为坐标原点)的垂直平分线上,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
已知函数 是定义域为
是定义域为 的奇函数,那么
的奇函数,那么 .
.
若不等式组 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则
分为面积相等的两部分,则 的值是 .
的值是 .
过原点且倾斜角为 的直线被圆
的直线被圆 所截得的弦长为 .
所截得的弦长为 .
已知数列 是等差数列,若
是等差数列,若 ,
, ,且数列
,且数列 的前
的前 项和
项和 有最大值,那么当
有最大值,那么当 取得最大值时,
取得最大值时, 等于 .
等于 .
(本小题满分12分)已知等比数列 的公比
的公比 ,
, ,
, ,等差数列
,等差数列 中
中 ,
, ,其中
,其中 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设数列 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)已知 ,
, 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本小题满分12分)某学校就一问题进行内部问卷调查.已知该学校有男学生 人,女学生
人,女学生 人,教师
人,教师 人,用分层抽样的方法从中抽取
人,用分层抽样的方法从中抽取 人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
人进行问卷调查.问卷调查的问题设置为“同意”、“不同意”两种,且每人都做一种选择.下面表格中提供了被调查人答卷情况的部分信息.
(1)请完成此统计表;
(2)根据此次调查,估计全校对这一问题持“同意”意见的人数;
(3)从被调查的女学生中选取 人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
人进行访谈,求选到两名学生中恰有一人“同意”、一人“不同意”的概率.
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)已知椭圆 (
( )的离心率为
)的离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆的标准方程;
(2)设 关于
关于 轴的对称点为
轴的对称点为 ,已知
,已知 为椭圆的上顶点,直线
为椭圆的上顶点,直线 ,
, 分别交
分别交 轴于点
轴于点 ,
, ,求
,求 的值.
的值.
(本小题满分14分)
设 ,
, 是函数
是函数 的两个极值点,且
的两个极值点,且 ,
, 且
且 .
.
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)求证: 为定值;
为定值;
(3)求 的取值范围.
的取值范围.