已知 ,
, ,则
,则 .
.
函数 的最小正周期为 .
的最小正周期为 .
复数 满足
满足

 (
( 是虚数单位),则
是虚数单位),则 .
.
函数 的定义域为 .
的定义域为 .
执行如图所示的流程图,则输出的 为 .
为 .
若数据 的方差为
的方差为 ,则
,则 .
.
袋子里有两个不同的红球和两个不同的白球,从中任取两个球,则这两个球颜色相同的概率为 .
等比数列 中,
中, ,
, ,则数列的前
,则数列的前 项和为 .
项和为 .
已知函数 是奇函数,则
是奇函数,则 .
.
双曲线 的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的
的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的
离心率 .
.
若 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线 ,则在平面
,则在平面 内,一定不存在与直线
内,一定不存在与直线 平行的直线.
平行的直线.
②若直线 ,则在平面
,则在平面 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线 垂直.
垂直.
③若直线 ,则在平面
,则在平面 内,不一定存在与直线
内,不一定存在与直线 垂直的直线.
垂直的直线.
④若直线 ,则在平面
,则在平面 内,一定存在与直线
内,一定存在与直线 垂直的直线.
垂直的直线.
已知实数 满足
满足 ,
, ,则
,则 的取值范围为 .
的取值范围为 .
在 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 且
且 ,则
,则 面积的最大值为 .
面积的最大值为 .
在梯形 中,
中, ,
, ,
, 为梯形
为梯形 所在平面上一点,且满足
所在平面上一点,且满足 =0,
=0, ,
, 为边
为边 上的一个动点,则
上的一个动点,则 的最小值为 .
的最小值为 .
在平面直角坐标系 中,角
中,角 的终边经过点
的终边经过点 .
.
(1)求 的值;
的值;
(2)若 关于
关于 轴的对称点为
轴的对称点为 ,求
,求 的值.
的值.
如图,在多面体 中,四边形
中,四边形 是菱形,
是菱形, 相交于点
相交于点 ,
, ,
, ,平面
,平面
 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:直线
 平面
平面 .
.
如图,我市有一个健身公园,由一个直径为2km的半圆和一个以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 构成,其中
构成,其中 为
为 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道 ,按实际需要,四边形
,按实际需要,四边形 的两个顶点
的两个顶点 分别在线段
分别在线段 上,另外两个顶点
上,另外两个顶点 在半圆上,
在半圆上,  ,且
,且 间的距离为1km.设四边形
间的距离为1km.设四边形 的周长为
的周长为 km.
km.
(1)若 分别为
分别为 的中点,求
的中点,求 长;
长;
(2)求周长 的最大值.
的最大值.
如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
数列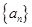 ,
,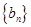 ,
,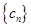 满足:
满足: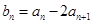 ,
, ,
, .
.
(1)若数列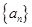 是等差数列,求证:数列
是等差数列,求证:数列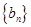 是等差数列;
是等差数列;
(2)若数列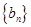 ,
,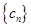 都是等差数列,求证:数列
都是等差数列,求证:数列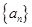 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列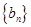 是等差数列,试判断当
是等差数列,试判断当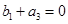 时,数列
时,数列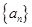 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
已知函数 ,
,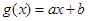 .
.
(1)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若直线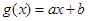 是函数
是函数 图象的切线,求
图象的切线,求 的最小值;
的最小值;
(3)当 时,若
时,若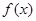 与
与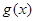 的图象有两个交点
的图象有两个交点 ,求证:
,求证: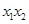
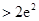 .(取
.(取 为
为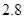 ,取
,取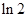 为
为 ,取
,取 为
为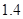 )
)