集合A＝{－1,0，2}，B＝{x｜｜x｜＜1}，则A
B＝
已知i是虚数单位，则
的实部为
命题P：“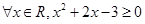
”，命题P的否定：
在三张奖券中有一、二等奖各一张，另一张无奖，甲乙两人各抽取一张（不放回），两人都中奖的概率为
如图是一个算法流程图，输出的结果为
已知样本6，7，8，9，m的平均数是8，则标准差是
实数x，y满足
，则
的最小值为
已知
，则
＝
已知双曲线C：
的一条渐近线与直线l：
＝0垂直，且C的一个焦点到l的距离为2，则C的标准方程为
设函数
，若f（x）的值域为R，是实数a的取值范围是
已知
是单位圆上任一点，将射线OA绕点O逆时针旋转
到OB交单位圆于点
,已知
若
的最大值为3，则
设实数x，y满足x2＋2xy－1＝0，则x2＋y2的最小值是
设数列{
}的前n项和为Sn，且
，若对任意
，都有
，则实数p的取值范围是
已知A（0,1），曲线C：y＝logax恒过点B，若P是曲线C上的动点，且
的最小值为2，则a＝
已知函数
部分图象如图所示。
（1）求函数
的解析式；
（2）当
时，求函数
的值域。
在三棱锥P－ABC中，D为AB的中点。
（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：
（2）若PA＝PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC。
如图，A，B，C是椭圆M：
上的三点，其中点A是椭圆的右顶点，BC过椭圆M的中心，且满足AC⊥BC，BC＝2AC。
（1）求椭圆的离心率；
（2）若y轴被△ABC的外接圆所截得弦长为9，求椭圆方程。
如图，某商业中心O有通往正东方向和北偏东30º方向的两条街道，某公园P位于商业中心北偏东
角（
），且与商业中心O的距离为
公里处，现要经过公园P修一条直路分别与两条街道交汇于A，B两处。
（1）当AB沿正北方向时，试求商业中心到A，B两处的距离和；
（2）若要使商业中心O到A，B两处的距离和最短，请确定A，B的最佳位置。
已知数列{
}中，
，且
对任意正整数都成立，数列{}的前n项和为Sn。
（1）若
，且
，求a；
（2）是否存在实数k，使数列{}是公比不为1的等比数列，且任意相邻三项
按某顺序排列后成等差数列，若存在，求出所有k值，若不存在，请说明理由；
（3）若
。
已知函数
。
（1）若f（x）的图象与g（x）的图象所在两条曲线的一个公共点在y轴上，且在该点处两条曲线的切线互相垂直，求b和c的值。
（2）若a＝c＝1，b＝0，试比较f（x）与g（x）的大小，并说明理由；
（3）若b＝c＝0，证明：对任意给定的正数a，总存在正数m，使得当x
时，
恒有f（x）＞g（x）成立。