下列方程是一元二次方程的是( )
A.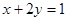 |
B. |
C.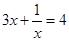 |
D.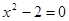 |
若关于x的方程(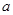 -1)x
-1)x =1是一元二次方程,则
=1是一元二次方程,则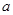 的值是( )
的值是( )
| A.0 | B.-1 | C.±1 | D.1 |
把方程(x-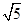 )(x+
)(x+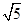 )+(2x-1)2=0化为一元二次方程的一般形式是( )
)+(2x-1)2=0化为一元二次方程的一般形式是( )
| A.5x2-4x-4=0 | B.x2-5=0 | C.5x2-2x+1=0 | D.5x2-4x+6=0 |
方程x2=6x的根是( )
| A.x1=0,x2=-6 | B.x1=0,x2=6 | C.x=6 | D.x=0 |
已知点(a,8)在二次函数y=a x2的图象上,则a的值是( )
| A.2 | B.-2 | C.±2 | D.±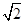 |
已知h关于t的函数关系式为h= gt2(g为正常数,t为时间), 则如图中函数的图像为( )
gt2(g为正常数,t为时间), 则如图中函数的图像为( )
某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
| A.200(1+x)2=1000 |
| B.200+200×2x=1000 |
| C.200+200×3x=1000 |
| D.200[1+(1+x)+(1+x)2]=1000 |
二次函数y=-2x2+3的开口方向是_________.
若关于x的方程(k-1)x2-4x+5="0" 有实数根, 则k 的取值范围是_______.
函数y=9-4x2,的顶点坐标是________.
如果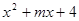 是一个完全平方公式,则
是一个完全平方公式,则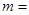
若y=(2-m)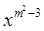 是二次函数,且开口向上,则
是二次函数,且开口向上,则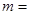
若一元二次方程ax2+bx+c=0(a≠0)有一个根为1,则a+b+c= .
若分式方程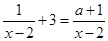 有增根,则a的值是 .
有增根,则a的值是 .
平行四边形两邻角的平分线相交所成的角为_________.
解下列方程.
(1)5x(x-3)="6-2x;"
(2)3y2 +7y-3=0
(3)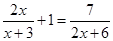 ;
;
试说明关于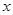 的方程
的方程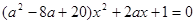 无论
无论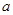 取何值,该方程都是一元二次方程。
取何值,该方程都是一元二次方程。
已知关于x的一元二次方程x2+2x+m=0.
(1)当m=3时,判断方程的根的情况;
(2)当m=-3时,求方程的根.
如图,已知点A(-4,8)和点B(2,n)在抛物线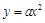 上.求a的值及点B的坐标.
上.求a的值及点B的坐标. 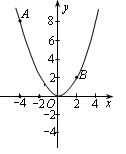
如图,在□ABCD中,E,F分别为边AB,CD的中点,连结DE,BF,BD.
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米。设这个苗圃园垂直于墙的一边的长为x米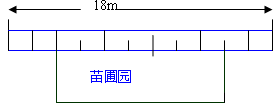
(1)用含x的代数式表示平行于墙的一边的长为____米,.x的取值范围为____
(2)这个苗圃园的面积为88平方米时,求x的值
某工程队在我城中村拆迁改造过程中承包了一项拆迁工程,原计划每天拆迁1250平方米,应准备工作不足,第一天少拆迁了20% 。从第二天起,该工程对加快了拆迁速度,第三天拆迁了1440平方米,
(1)求:该工程队第一天拆迁的面积;
(2)若该工程队第二天,第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数
如图,直线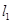 的解析表达式为
的解析表达式为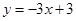 ,且
,且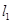 与
与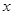 轴交于点
轴交于点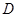 ,直线
,直线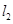 经过点
经过点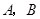 ,直线
,直线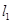 ,
,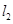 交于点
交于点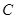 .
.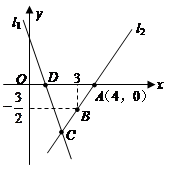
(1)求点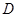 的坐标;
的坐标;
(2)求直线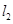 的解析表达式;
的解析表达式;
(3)求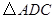 的面积。
的面积。
如图,在直角梯形ABCD中,AD∥CB, 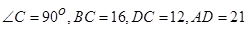 ,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形ABQP是平行四边形.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?