已知全集 , 集合
, 集合 ,
,  , 则集合
, 则集合 可以表示为( )
可以表示为( )
A. |
B. |
C. |
D. |
已知向量 ,若
,若 ,则实数
,则实数 的值为( )
的值为( )
A. |
B. |
C. |
D. |
若某市 所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
A. |
B. |
C. |
D. |
已知 为虚数单位,复数
为虚数单位,复数
 的虚部
的虚部 记作
记作
 ,则
,则
 ( )
( )
A. |
B. |
C. |
D. |
设抛物线
 上一点
上一点 到
到 轴的距离为
轴的距离为 ,则点
,则点 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )
A. |
B. |
C. |
D. |
已知△ 的三边
的三边 所对的角分别为
所对的角分别为 ,且
,且 , 则
, 则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
已知数列 为等比数列,若
为等比数列,若 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
若直线 上存在点
上存在点 满足约束条件
满足约束条件 则实数
则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知某锥体的正视图和侧视图如图2,其体积为 ,则该锥体的俯视图可以是( )
,则该锥体的俯视图可以是( )

已知圆 的圆心为坐标原点,半径为
的圆心为坐标原点,半径为 ,直线
,直线 为常数,
为常数, 与圆
与圆 相交于
相交于 两点,记△
两点,记△ 的面积为
的面积为 ,则函数
,则函数 的奇偶性为( )
的奇偶性为( )
| A.偶函数 | B.奇函数 |
| C.既不是偶函数,也不是奇函数 | D.奇偶性与 的取值有关 的取值有关 |
函数 的定义域为 .
的定义域为 .
已知e为自然对数的底数,则曲线 e
e 在点
在点 处的切线斜率为 .
处的切线斜率为 .
已知函数 ,点
,点 为坐标原点, 点
为坐标原点, 点 N
N , 向量
, 向量 ,
, 是向量
是向量 与
与 的夹角,则
的夹角,则 的值为 .
的值为 .
(坐标系与参数方程选讲选做题)在直角坐标系 中,曲线
中,曲线 和
和 的参数方程分别为
的参数方程分别为 为参数
为参数 和
和 为参数
为参数 .以原点
.以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,则曲线
轴正半轴为极轴,建立极坐标系,则曲线 与
与 的交点的极坐标为 .
的交点的极坐标为 .
(几何证明选讲选做题)如图, 是圆
是圆 的一条弦,延长
的一条弦,延长 至点
至点 ,使得
,使得 ,过
,过 作圆
作圆 的切线,
的切线, 为切点,
为切点, 的平分线
的平分线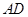 交
交 于点
于点 ,则
,则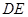 的长为 .
的长为 . 
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若 是第一象限角,且
是第一象限角,且 ,求
,求 的值.
的值.
(本小题满分12分)从广州某高校男生中随机抽取 名学生,测得他们的身高(单位: cm)情况如表1:
名学生,测得他们的身高(单位: cm)情况如表1:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 合计 |
 |
 |
表1
(1)求 的值;
的值;
(2)按表1的身高组别进行分层抽样, 从这 名学生中抽取
名学生中抽取 名担任广州国际马拉松志愿者, 再从身高不低于
名担任广州国际马拉松志愿者, 再从身高不低于 cm的志愿者中随机选出
cm的志愿者中随机选出 名担任迎宾工作, 求这
名担任迎宾工作, 求这 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有 名的身高不低于
名的身高不低于 cm的概率.
cm的概率.
(本小题满分14分)如图,在边长为 的菱形
的菱形 中,
中, ,点
,点 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, .沿
.沿 将△
将△ 翻折到△
翻折到△ ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
(本小题满分14分)已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
,  ,
,  N
N .
.
(1)求 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在正整数 ,使
,使 ,
, ,
,  成等比数列? 若存在,求
成等比数列? 若存在,求 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
(本小题满分14分)已知椭圆 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线 的顶点,直线
的顶点,直线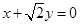 与椭圆
与椭圆 交于
交于 ,
, 两点,且点
两点,且点 的坐标为
的坐标为 ,点
,点 是椭圆
是椭圆 上异于点
上异于点 ,
, 的任意一点,点
的任意一点,点 满足
满足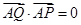 ,
, ,且
,且 ,
, ,
, 三点不共线.
三点不共线.
(1)求椭圆 的方程;
的方程;
(2)求点 的轨迹方程;
的轨迹方程;
(3)求 面积的最大值及此时点
面积的最大值及此时点 的坐标.
的坐标.
(本小题满分14分)已知 为常数,且
为常数,且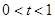 ,函数
,函数 的最小值和函数
的最小值和函数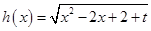 的最小值都是函数
的最小值都是函数
 R
R 的零点.
的零点.
(1)用含 的式子表示
的式子表示 ,并求出
,并求出 的取值范围;
的取值范围;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.