已知全集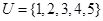 ,
,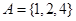 ,
,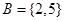 ,则
,则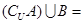 ( )
( )
A.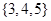 |
B.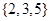 |
C.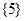 |
D.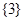 |
 ( )
( )
A.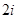 |
B.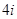 |
C.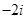 |
D.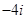 |
已知抛物线的焦点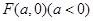 ,则抛物线的标准方程是( )
,则抛物线的标准方程是( )
A.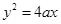 |
B.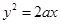 |
C.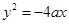 |
D.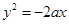 |
命题P: ;命题q:
;命题q: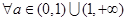 ,函数
,函数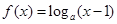 的图象过点
的图象过点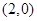 ,则( )
,则( )
| A.P假q真 | B.P真q假 | C.P假q假 | D.P真q真 |
执行下边的程序框图,则输出的A是( )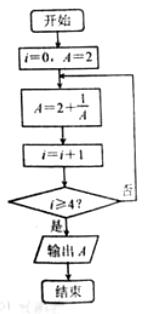
A.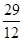 |
B.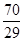 |
C.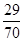 |
D.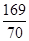 |
设x,y满足约束条件 ,则
,则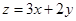 的最大值为( )
的最大值为( )
| A.8 | B.9 | C.28 | D.29 |
在直角梯形ABCD中,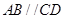 ,
,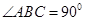 ,
,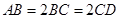 ,则
,则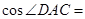 ( )
( )
A. |
B. |
C.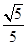 |
D.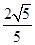 |
某几何体的三视图如图所示,则该几何体的体积为( )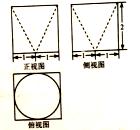
A.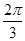 |
B.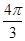 |
C.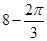 |
D.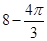 |
已知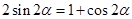 ,则
,则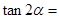 ( )
( )
A.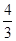 |
B.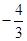 |
C.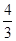 或0 或0 |
D.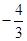 或0 或0 |
函数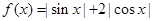 的值域为( )
的值域为( )
A.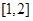 |
B. |
C.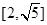 |
D.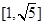 |
F是双曲线C: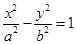
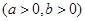 的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若
的右焦点,过点F向C的一条渐近线引垂直,垂足为A,交另一条渐近线于点B,若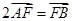 ,则C的离心率是( )
,则C的离心率是( )
A.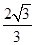 |
B.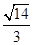 |
C.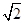 |
D.2 |
直线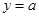 分别与曲线
分别与曲线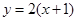 ,
,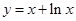 交于A,B,则
交于A,B,则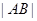 的最小值为( )
的最小值为( )
| A.3 | B.2 | C.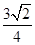 |
D.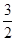 |
函数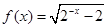 的定义域是 .
的定义域是 .
已知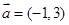 ,
,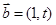 ,若
,若 ,则
,则 .
.
一枚质地均匀的正方体玩具,四个面标有数字1,其余两个面标有数字2,抛掷两次,所得向上数字相同的概率是 .
在半径为2的球面上有不同的四点A、B、C、D,若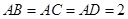 ,则平面BCD被球所截面图形的面积为 .
,则平面BCD被球所截面图形的面积为 .
(本小题满分12分)设数列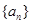 的前n项和为
的前n项和为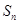 ,满足
,满足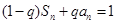 ,且
,且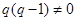 .
.
(Ⅰ)求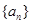 的通项公式;
的通项公式;
(Ⅱ)若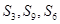 成等差数列,求证:
成等差数列,求证: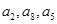 成等差数列.
成等差数列.
(本小题满分12分)
为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据:
| 天数t(天) |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y(千个) |
2.5 |
3 |
4 |
4.5 |
6 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,预测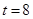 时,细菌繁殖个数.
时,细菌繁殖个数.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: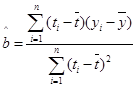 ,
,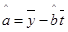 .
.
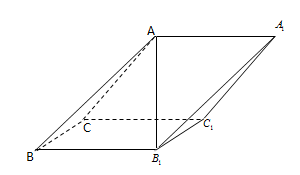
(本小题满分12分)如图,在斜三棱柱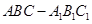 中,侧面
中,侧面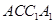 与侧面
与侧面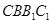 都是菱形,
都是菱形, ,
,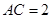 .
.
(Ⅰ)求证: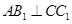 ;
;
(Ⅱ)若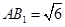 ,求四棱锥
,求四棱锥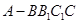 的体积.
的体积.
(本小题满分12分)已知圆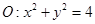 ,点
,点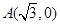 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆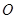 ,记点B的轨迹为
,记点B的轨迹为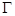 .
.
(Ⅰ)求曲线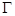 的方程;
的方程;
(Ⅱ)直线AB交圆 于C,D两点,当B为CD中点时,求直线AB的方程.
于C,D两点,当B为CD中点时,求直线AB的方程.
(本小题满分12分)已知函数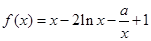 ,
,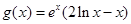 .
.
(Ⅰ)若函数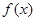 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围;
(Ⅱ)求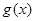 的最大值.
的最大值.
(本小题满分10分)如图,圆周角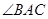 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.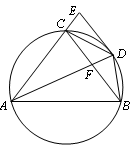
(Ⅰ)求证: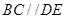 ;
;
(Ⅱ)若D,E,C,F四点共圆,且弧长AC等于弧长BC,求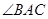 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: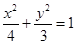 ,直线
,直线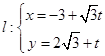 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线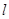 的普通方程;
的普通方程;
(Ⅱ)设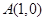 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线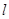 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
(本小题满分10分)选修4-5:不等式选讲
已知函数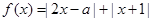 .
.
(Ⅰ)当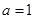 时,解不等式
时,解不等式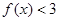 ;
;
(Ⅱ)若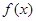 的最小值为1,求a的值.
的最小值为1,求a的值.