已知倾斜角为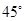 的直线经过
的直线经过 ,
,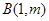 两点,则
两点,则 ( )
( )
A.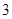 |
B. |
C. |
D.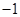 |
命题“若 ,则
,则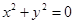 ”与它的逆命题、否命题、逆否命题中,真命题的个数为( )
”与它的逆命题、否命题、逆否命题中,真命题的个数为( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D.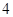 个 个 |
半径为 的半圆卷成一个圆锥,圆锥的体积为( )
的半圆卷成一个圆锥,圆锥的体积为( )
A. |
B. |
C. |
D. |
四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )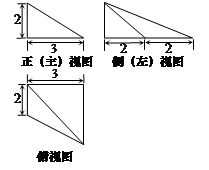
A. |
B.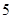 |
C. |
D.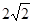 |
已知三条直线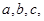 若
若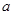 和
和 是异面直线,
是异面直线, 和
和 是异面直线,那么直线
是异面直线,那么直线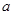 和
和 的位置关系是( )
的位置关系是( )
| A.平行 | B.相交 | C.异面 | D.平行、相交或异面 |
若焦距为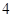 的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为( )
的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为( )
A. |
B. |
C.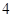 |
D.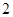 |
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 则 则 |
B.若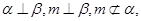 则 则 |
C.若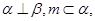 则 则 |
D.若 则 则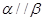 |
如果实数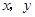 满足
满足 ,那么
,那么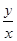 的最大值是
的最大值是
A. |
B. |
C.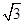 |
D. |
如图,正方体 的棱长为
的棱长为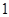 ,线段
,线段 上有两个动点
上有两个动点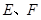 ,且
,且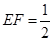 ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A. |
B. 平面 平面 |
C.三棱锥 的体积为定值 的体积为定值 |
D. 的面积与 的面积与 的面积相等 的面积相等 |
椭圆 上的两点
上的两点 关于直线
关于直线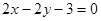 对称,则弦
对称,则弦 的中点坐标为( )
的中点坐标为( )
A. |
B. |
C. |
D.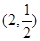 |
命题“ ,
, ”的否定形式为 ;
”的否定形式为 ;
对于任意实数 ,直线
,直线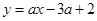 所经过的定点是 ;
所经过的定点是 ;
若圆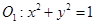 与圆
与圆 内切,则
内切,则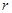 的值为_______;
的值为_______;
抛物线 上与其焦点的距离等于
上与其焦点的距离等于 的点的坐标是 ;
的点的坐标是 ;
双曲线 与椭圆
与椭圆 的中心在原点,其公共焦点
的中心在原点,其公共焦点 在
在 轴上,点
轴上,点 是
是 在第一象限的公共点.若
在第一象限的公共点.若 ,
, 的离心率是
的离心率是 ,则双曲线
,则双曲线 的渐近线方程是 .
的渐近线方程是 .
已知直线 ,
, .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)当 时,求直线
时,求直线 与
与 之间的距离.
之间的距离.
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,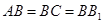 ,
,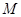 是
是 的中点,
的中点, 是
是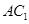 与
与 的交点.
的交点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: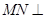 平面
平面 .
.
已知命题 方程
方程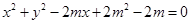 表示圆;命题
表示圆;命题 双曲线
双曲线 的离心率
的离心率 ,若命题“
,若命题“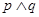 ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数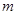 的取值范围.
的取值范围.
如图,在矩形 中,点
中,点 为边
为边 上的点,点
上的点,点 为边
为边 的中点,
的中点,  ,现将
,现将 沿
沿 边折至
边折至 位置,且平面
位置,且平面 平面
平面 .
.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求四棱锥 的体积.
的体积.
已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)求过点
 的圆
的圆 的切线方程;
的切线方程;
(Ⅲ)已知 ,点
,点 在圆
在圆 上运动,求以
上运动,求以 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹
轨迹
方程.
已知椭圆 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知 为椭圆
为椭圆 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.