已知集合 ,
,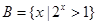 ,则
,则
A.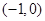 |
B.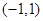 |
C. |
D. |
复数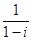 (
( 是虚数单位)的虚部是
是虚数单位)的虚部是
A.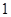 |
B. |
C. |
D.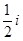 |
设 ,
,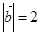 ,且
,且 夹角
夹角 ,则
,则
A. |
B. |
C. |
D. |
从数字 、
、 、
、 、
、 、
、 中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为
中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为
A. |
B.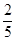 |
C.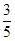 |
D. |
已知等差数列 的前
的前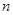 项和为
项和为 ,若
,若 ,则
,则
A.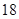 |
B. |
C. |
D.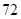 |
某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的 的值是
的值是
| A.2 | B. |
C. |
D.3 |
如图,程序输出的结果 , 则判断框中应填
, 则判断框中应填
A. |
B.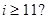 |
C. |
D. |
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,
是两个不同的平面,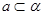 ,
, ,则
,则 ∥
∥ 是
是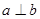 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
已知不等式组 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 有公共点,则
有公共点,则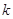 的取值范围为是
的取值范围为是
A. |
B. |
C. |
D. |
在直角坐标系 中,设
中,设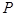 是曲线
是曲线 :
: 上任意一点,
上任意一点, 是曲线
是曲线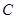 在点
在点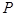 处的切线,且
处的切线,且 交坐标轴于
交坐标轴于 ,
,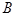 两点,则以下结论正确的是
两点,则以下结论正确的是
A.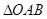 的面积为定值 的面积为定值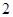 |
B.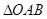 的面积有最小值为 的面积有最小值为 |
C.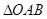 的面积有最大值为 的面积有最大值为 |
D.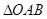 的面积的取值范围是 的面积的取值范围是 |
已知抛物线 :
: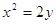 的焦点为
的焦点为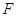 ,以
,以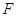 为圆心的圆
为圆心的圆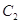 交
交 于
于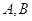 两点,交
两点,交 的准线于
的准线于 两点,若四边形
两点,若四边形 是矩形,则圆
是矩形,则圆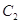 的标准方程为
的标准方程为
A. |
B.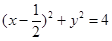 |
C. |
D. |
己知定义在 上的可导函数
上的可导函数 的导函数为
的导函数为 ,满足
,满足 ,且
,且 为偶函数,
为偶函数, ,则不等式
,则不等式 的解集为
的解集为
A. |
B. |
C.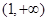 |
D.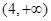 |
已知 ,
, ,则
,则 .
.
椭圆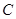 的中心在原点,焦点在
的中心在原点,焦点在 轴上,若椭圆
轴上,若椭圆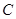 的离心率等于
的离心率等于 ,且它的一个顶点恰好是抛物线
,且它的一个顶点恰好是抛物线 的焦点,则椭圆
的焦点,则椭圆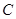 的标准方程为 .
的标准方程为 .
已知函数 有两个极值点,则实数
有两个极值点,则实数 的取值范围是 .
的取值范围是 .
数列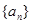 的首项为
的首项为 ,数列
,数列 为等比数列且
为等比数列且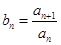 ,若
,若 ,则
,则 .
.
(本小题满分12分)在 中,角
中,角 、
、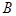 、
、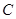 所对的边分别为
所对的边分别为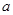 、
、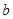 、
、 ,已知
,已知 .
.
(1)求 的大小;
的大小;
(2)若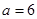 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形,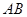 ∥
∥ ,
, ,
,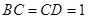 ,顶点
,顶点 在底面
在底面 内的射影恰为点
内的射影恰为点 .
.
(1)求证: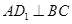 ;
;
(2)若直线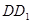 与直线
与直线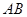 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的
所成角(锐角)的
余弦函数值.
(本小题满分12分)为迎接2015年在兰州举行的“中国兰州国际马拉松赛”,某单位在推介晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的 个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取
个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取 次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为
次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为 .
.
(1)求盒中印有“兰州马拉松”标志的小球个数;
(2)用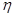 表示某位嘉宾抽奖的次数,求
表示某位嘉宾抽奖的次数,求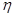 的分布列和期望.
的分布列和期望.
(本小题满分12分)
已知双曲线 :
: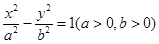 的一条渐近线为
的一条渐近线为 ,右焦点
,右焦点 到直线
到直线 的距离为
的距离为 .
.
(1)求双曲线 的方程;
的方程;
(2)斜率为 且在
且在 轴上的截距大于
轴上的截距大于 的直线
的直线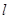 与曲线
与曲线 相交于
相交于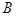 、
、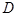 两点,已知
两点,已知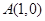 ,若
,若 证明:过
证明:过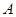 、
、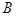 、
、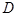 三点的圆与
三点的圆与 轴相切.
轴相切.
(本小题满分12分)设函数 .
.
(1)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的取值范围;
的取值范围;
(2)若 ,试比较当
,试比较当 时,
时, 与
与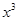 的大小;
的大小;
(3)证明:对任意的正整数 ,不等式
,不等式 成立.
成立.
(本小题满分10分)选修4—1:几何证明选讲
如图,已知 切⊙
切⊙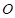 于点
于点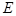 ,割线
,割线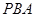 交⊙
交⊙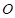 于
于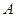 、
、 两点,
两点,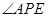 的平分线和
的平分线和 、
、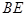 分别交于点
分别交于点 、
、 .求证:
.求证:
(1) ;
;
(2) .
.
(本小题满分10分)选修4-4:极坐标系与参数方程
在直角坐标系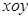 中,曲线
中,曲线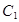 的参数方程为
的参数方程为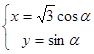 ,(
,( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为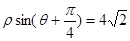 .
.
(1)求曲线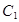 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线 上的动点,求点
上的动点,求点 到
到 上点的距离的最小值.
上点的距离的最小值.
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数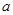 的值;
的值;
(2)在(1)的条件下,若存在实数 使
使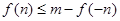 成立,求实数
成立,求实数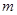 的取值范围.
的取值范围.