若
为虚数单位，则
的值为（ ）
A． |
B． |
C． |
D． |
若全集
，
，
，则集合
等于（ ）
A． |
B． |
C． |
D． |
若双曲线的标准方程为
，则它的渐近线方程为（ ）
A． |
B． |
C． |
D． |
已知命题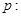
，
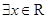，命题
，
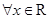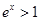，则（ ）
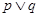A．命题 是假命题 |
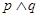B．命题 是真命题 |
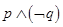C．命题 是真命题 |
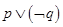D．命题 是假命题 |
在
中，角
，
，
的对边分别为
，
，
，且
，
，
，则的值为（ ）
A． |
B． |
C． |
D． |
设
，
，
为平面，
，
为直线，则
的一个充分条件是（ ）
A． ， ， |
B． ， ， |
C．，， |
D． ， ， |
已知等差数列
的前
项和为
，又知
，且
，
，则
为（ ）
A． |
B． |
C． |
D． |
气象意义上从春季进入夏季的标志为：“连续
天的日平均温度均不低于
”．现有甲、乙、丙三地连续天的日平均温度的记录数据（记录数据都是正整数）：
①甲地：个数据的中位数为
，众数为；
②乙地：个数据的中位数为
，总体均值为；
③丙地：个数据中有一个数据是
，总体均值为
，总体方差为
．
则肯定进入夏季的地区有（ ）
| A．①②③ | B．①③ | C．②③ | D．① |
把二进制数
化为十进制数，结果为 ．
设空间向量
，
，且
，则
，
．
二项展开式
中，含
项的系数为 ．
一元二次不等式
的解集为
，则一元一次不等式
的解集为 ．
已知实数
，
满足
，若目标函数
的最大值为
，最小值为
，则实数
的取值范围是 ．
（坐标系与参数方程选做题）曲线
（
为参数），若以点
为极点，
轴正半轴为极轴建立极坐标系，则该曲线的极坐标方程是 ．
（几何证明选讲选做题）如图，
是
的高，
是外接圆的直径，若
，则
．
（本小题满分12分）已知函数
．
（1）求
的值；
（2）判断并证明函数
的奇偶性；
（3）设
为第四象限的角，且
，求
的值．
（本小题满分12分）某中学一名数学老师对全班
名学生某次考试成绩分男女生进行了统计（满分
分），其中
分（含分）以上为优秀，绘制了如下的两个频率分布直方图：
（1）根据以上两个直方图完成下面的
列联表：
（2）根据（1）中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？
（3）若从成绩在
的学生中任取
人，求取到的人中至少有
名女生的概率．
（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其中正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．
（1）求证：
平面
；
（2）设
为直线
与平面
所成的角，求
的值；
（3）设
为
中点，在
边上求一点
，使
平面，求
的值．
（本小题满分14分）在平面直角坐标系
中，已知动点
到两个定点
，
的距离的和为定值
．
（1）求点运动所成轨迹
的方程；
（2）设
为坐标原点，若点
在轨迹上，点
在直线
上，且
，试判断直线
与圆
的位置关系，并证明你的结论．
（本小题满分14分）已知
是数列
的前
项和，且满足
（
，
），又已知
，
，
，
，
，
．
计算
，
，并求数列
的通项公式；
若
，
为数列
的前项和，求证：
．
（本小题满分14分）设函数
（
）．
（1）当
时，求过点
且与曲线
相切的切线方程；
（2）求函数
的单调递增区间；
（3）若函数有两个极值点
，
，且
，记
表示不大于
的最大整数，试比较
与
的大小．