若集合 ,
, ,则集合
,则集合 ( )
( )
A. |
B. |
C. |
D. |
在 中,
中, ,
, ,
, ,则( )
,则( )
A. 或 或 |
B. |
C. |
D.以上答案都不对 |
在复平面内,复数 ,
, 对应的点分别为
对应的点分别为 ,
, ,则线段
,则线段 的中点
的中点 对应的复数为( )
对应的复数为( )
A. |
B. |
C. |
D. |
已知变量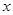 与
与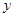 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,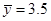 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.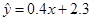 |
B.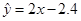 |
C.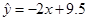 |
D.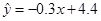 |
下列函数中,是偶函数,且在区间 内单调递增的函数是( )
内单调递增的函数是( )
A. |
B. |
C. |
D. |
一个锥体的主视图和左视图如下图所示,下面选项中,不可能是该锥体的俯视图的是( )

若抛物线 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则该抛物线的准线方程为( )
的右焦点重合,则该抛物线的准线方程为( )
A. |
B. |
C. |
D. |
如图所示的程序框图,若输出的 ,则判断框内应填入的条件是( )
,则判断框内应填入的条件是( )
A. |
B. |
C. |
D. |
下列命题中正确的是( )
A.若 为真命题,则 为真命题,则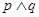 为真命题 为真命题 |
B.“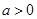 , ,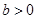 ”是“ ”是“ ”的充分必要条件 ”的充分必要条件 |
C.命题“若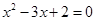 ,则 ,则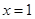 或 或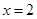 ”的逆否命题为“若 ”的逆否命题为“若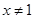 或 或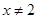 ,则 ,则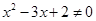 ” ” |
D.命题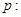 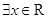 ,使得 ,使得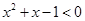 ,则 ,则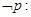 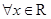 ,使得 ,使得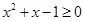 |
在整数集 中,被
中,被 除所得余数为
除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,即
,即 ,
, ,
, ,
, ,
, ,
, .给出如下四个结论:
.给出如下四个结论:
① ;
;
② ;
;
③ ;
;
④整数 ,
, 属于同一“类”的充要条件是“
属于同一“类”的充要条件是“ ”.
”.
其中,正确结论的个数是( )
A. |
B. |
C. |
D. |
已知数列 为等差数列,
为等差数列, ,
, ,则
,则 .
.
已知向量 ,
, 的夹角为
的夹角为 ,且
,且 ,
, ,则
,则
已知实数 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
(坐标系与参数方程选做题)在极坐标系中,直线 被圆
被圆 截得的弦长为 .
截得的弦长为 .
(几何证明选讲选做题)如图, 是半圆的圆心,直径
是半圆的圆心,直径 ,
,  是圆的一条切线,割线
是圆的一条切线,割线 与半圆交于点
与半圆交于点 ,
, ,则
,则 .
.
(本小题满分12分)已知函数 ,
, .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 .
.
(本小题满分12分)为了解某市民众对某项公共政策的态度,在该市随机抽取了 名市民进行调查,做出了他们的月收入(单位:百元,范围:
名市民进行调查,做出了他们的月收入(单位:百元,范围: )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
(1)求月收入在 内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
(2)根据频率分布直方图估计这 人的平均月收入;
人的平均月收入;
(3)若从月收入(单位:百元)在 的被调查者中随机选取
的被调查者中随机选取 人,求
人,求 人都不赞成的概率.
人都不赞成的概率.
(本小题满分14分)如图,四边形 为菱形,
为菱形, 为平行四边形,且平面
为平行四边形,且平面 平面
平面 ,设
,设 与
与 相交于点
相交于点 ,
, 为
为 的中点.
的中点.
(1)证明: ;
;
(2)若 ,
, ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分14分)已知数列 的前
的前 项之和为
项之和为 (
( ),且满足
),且满足 .
.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)求证: .
.
(本小题满分14分)椭圆
 (
( )的左焦点为
)的左焦点为 ,右焦点为
,右焦点为 ,离心率
,离心率 .设动直线
.设动直线
 与椭圆
与椭圆 相切于点
相切于点 且交直线
且交直线 于点
于点 ,
, 的周长为
的周长为 .
.
(1)求椭圆 的方程;
的方程;
(2)求两焦点 、
、 到切线
到切线 的距离之积;
的距离之积;
(3)求证:以 为直径的圆恒过点
为直径的圆恒过点
(本小题满分14分)已知常数 ,函数
,函数 ,
, .
.
(1)讨论 在
在 上的单调性;
上的单调性;
(2)若 在
在 上存在两个极值点
上存在两个极值点 ,
, ,且
,且 ,求常数
,求常数 的取值范围.
的取值范围.