集合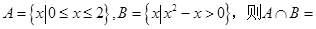 ( )
( )
| A.R | B.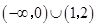 |
C.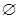 |
D. |
已知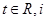 为虚数单位,复数
为虚数单位,复数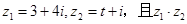 是实数,则t等于( )
是实数,则t等于( )
A.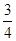 |
B.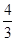 |
C.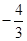 |
D.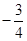 |
设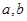 为实数,命题甲:
为实数,命题甲: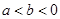 ,命题乙:
,命题乙: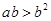 ,则命题甲是命题乙的( )
,则命题甲是命题乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知某几何体的三视图如图,则该几何体的表面积是( )
| A.24 | B.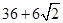 |
C.36 | D.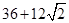 |
已知x,y满足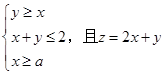 的最大值是最小值的4倍,则
的最大值是最小值的4倍,则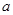 的值是( )
的值是( )
| A.4 | B.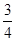 |
C.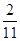 |
D.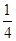 |
如图,在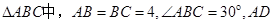 是边BC上的高,则
是边BC上的高,则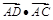 的值等于( )
的值等于( )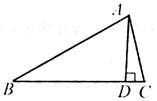
| A.0 | B.4 | C.8 | D.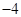 |
已知函数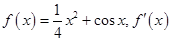 是函数
是函数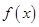 的导函数,则
的导函数,则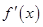 的图象大致是( )
的图象大致是( )
函数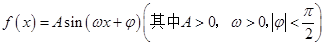 的图象如图所示,为了得到
的图象如图所示,为了得到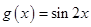 的图象,则只需将
的图象,则只需将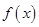 的图象( )
的图象( )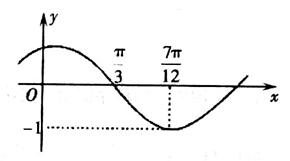
A.向左平移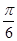 个长度单位 个长度单位 |
B.向右平移 个长度单位 个长度单位 |
C.向右平移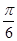 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
已知抛物线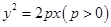 上一点
上一点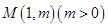 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线 的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
A.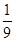 |
B.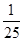 |
C.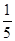 |
D.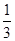 |
已知定义域为R的奇函数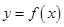 的导函数为
的导函数为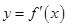 ,当
,当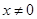 时,
时,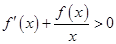 ,若
,若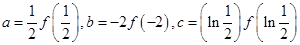 ,则
,则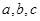 的大小关系正确的是( )
的大小关系正确的是( )
A.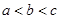 |
B.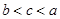 |
C.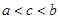 |
D.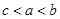 |
在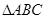 中,若
中,若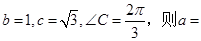 .
.
在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(下图),但是年龄组为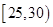 的数据不慎丢失,据此估计这800名志愿者年龄在
的数据不慎丢失,据此估计这800名志愿者年龄在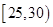 的人数为 .
的人数为 .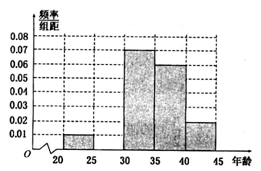
运行如右上图所示的程序框图,则输出的结果S为 .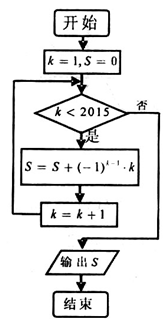
已知函数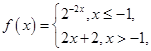 则满足
则满足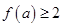 的实数a的取值范围是 .
的实数a的取值范围是 .
已知数集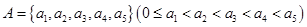 具有性质p:对任意
具有性质p:对任意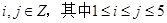 ,均有
,均有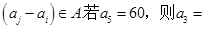 .
.
(本小题满分12分)某中学在高二年级开设大学先修课程《线性代数》,共有50名同学选修,其中男同学30名,女同学20名.为了对这门课程的教学效果进行评估,学校按性别采用分层抽样的方法抽取5人进行考核.
(1)求抽取的5人中男、女同学的人数;
(2)考核前,评估小组打算从抽取的5人中随机选出2名同学进行访谈,求选出的两名同学中恰有一名女同学的概率.
(本小题满分12分)已知函数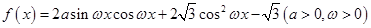 的最大值为2,且最小正周期为
的最大值为2,且最小正周期为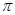 .
.
(1)求函数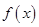 的解析式及其对称轴方程;
的解析式及其对称轴方程;
(2)若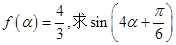 的值.
的值.
(本小题满分12分)如图,已知四边形ABCD是正方形, 平面ABCD,CD=PD=2EA,PD//EA,F,G,H分别为PB,BE,PC的中点.
平面ABCD,CD=PD=2EA,PD//EA,F,G,H分别为PB,BE,PC的中点.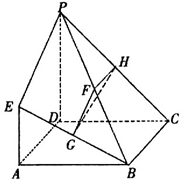
(1)求证:GH//平面PDAE;
(2)求证:平面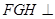 平面PCD.
平面PCD.
(本小题满分12分)已知数列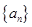 中,
中,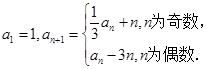
(1)证明数列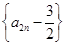 是等比数列;
是等比数列;
(2)若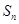 是数列
是数列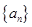 的前n项和,求
的前n项和,求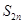 .
.
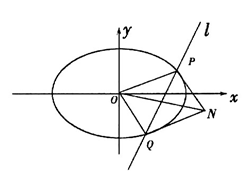
(本小题满分13分)已知椭圆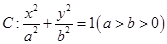 ,其中
,其中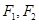 为左、右焦点,且离心率
为左、右焦点,且离心率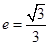 ,直线
,直线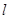 与椭圆交于两不同点
与椭圆交于两不同点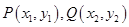 .当直线
.当直线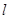 过椭圆C右焦点F2且倾斜角为
过椭圆C右焦点F2且倾斜角为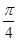 时,原点O到直线
时,原点O到直线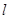 的距离为
的距离为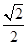 .
.
(1)求椭圆C的方程;
(2)若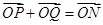 ,当
,当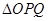 面积为
面积为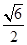 时,求
时,求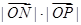 的最大值.
的最大值.
(本小题满分14分)已知函数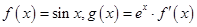 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求曲线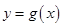 在点
在点 处的切线方程;
处的切线方程;
(2)若对任意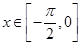 ,不等式
,不等式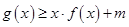 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试探究当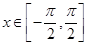 时,方程
时,方程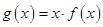 的解的个数,并说明理由.
的解的个数,并说明理由.