已知集合
，集合
，则
（ ）
A． |
B． |
C． |
D． |
已知
是虚数单位，若
，则
（ ）
A． |
B． |
C． |
D． |
下列函数中，在区间
上为增函数的是（ ）
A． |
B． |
C． |
D． |
抛物线
的焦点坐标是（ ）
A． |
B． |
C． |
D． |
将函数
的图象上所有的点向右平移
个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是（ ）
A． |
B． |
C． |
D． |
已知
，
，
为
的三个内角，命题
:
;命题
:
.则
是
的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
若直线
被圆
所截得的弦长为
，则
（ ）
A． 或 |
B． 或 |
C．或 |
D．或 |
已知向量
，
，
，若
∥
，则实数
的值为（ ）
A． |
B． |
C． |
D． |
对任意实数
、
，定义运算“⊙”：⊙
，设
⊙
，若函数
的图像与
轴恰有三个公共点，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
为椭圆
上任意一点，
为圆
的任意一条直径，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
已知直线
，
，若
，则
。
已知
，
，且点
在直线
上，则
的最小值为 .
设
，在约束条件
下，目标函数
的最大值等于
，则
.
已知
，
，则
.
若函数
在
上单调递增，则实数
的取值范围是 .
（本小题满分12分）设向量
，
，
。
（1）求的最小正周期；
（2）求在区间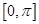
上的单调递减区间.
（本小题满分12分）公差
的等差数列
中，
，
、
、
成等比数列;
（1）求数列的通项公式;
（2）数列
满足
，求数列的通项公式.
（本小题满分12分）设为
的内角
、
、
所对的边分别为
、
、
，且
.
（1）求角的大小;
（2）若
，求
的取值范围.
（本小题满分13分）已知函数
，其中
.
（1）当
时，求
在
上的最大值;
（2）若
时，函数的最大值为
，求函数的表达式;
（本小题满分13分）已知数列
的前
项和为
，
，
.
（1）求数列的通项公式;
（2）求数列
的前项和
.
（本小题满分13分）已知椭圆
经过点
，离心率为
.
（1）求椭圆
的方程;
（2）设直线
与椭圆交于
、
，点关于
轴的对称点
（与不重合），则直线
与轴是否交于一定点?若是，请写出定点坐标，并证明你的结论;若不是，请说明理由.