已知全集
，集合
，
，则（∁U
）
（ ）
A． |
B． |
C． |
D． |
若
，则
是
的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
已知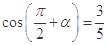
，且
，则
（ ）
A． |
B． |
C． |
D． |
某程序框图如图所示，该程序运行后输出的
的值是（ ）
| A．3 | B．4 | C．5 | D．6 |
某几何体三视图如下，其中三角形的三边长与圆的直径均为2，则该几何体体积为（ ）
A． |
B． |
C． |
D． |
设函数
，且其图像关于
轴对称，则函数
的一个单调递减区间是（ ）
A． |
B． |
C． |
D． |
已知
，则
展开式中，
的一次项系数为（ ）
A． |
B． |
C． |
D． |
抛物线
与双曲线
有相同焦点F，点A是两曲线交点，且
⊥
轴，则双曲线的离心率为（ ）
A． |
B． |
C． |
D． |
若曲线
与曲线
在它们的公共点
处具有公共切线，则实数
（ ）
A． |
B． |
C． |
D． |
已知定义在
上的奇函数
满足
，若
，
，则实数
的取值范围为（ ）
A． |
B． |
C． |
D． |
平面四边形
中，
,
,
,将其沿对角线
折成四面体
,使平面
平面
，若四面体的顶点在同一个球面上，则该球的体积为 （ ）
A． |
B． |
C． |
D． |
过抛物线
的焦点作两条互相垂直的弦
，则
（ ）
A． |
B． |
C． |
D． |
已知复数
，
是z的共轭复数，则
．
已知
为由不等式组
，所确定的平面区域上的动点，若点
，则
的最大值为 ．
已知点
为
的重心，过点作直线与
，
两边分别交于
两点，且
，则
．
在
中，内角
的对边分别为
，
已知，且
，则的面积是 ．
已知数列
满足
,
，
．
（1）求证：
是等差数列；
（2）证明：
．
如图，在三棱柱
中，已知
，
，
，
．
（1）求证：
；
（2）设
（
），且平面
与
所成的锐二面角的大小为30°，试求的值．
在一次考试中，5名同学数学、物理成绩如下表所示：
| 学生 |
A |
B |
C |
D |
E |
| 数学（x分） |
89 |
91 |
93 |
95 |
97 |
| 物理（y分） |
87 |
89 |
89 |
92 |
93 |
（1）根据表中数据，求物理分
对数学分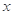
的回归方程：
（2）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以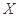
表示选中的同学中物理成绩高于90分的人数，求随机变量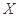的分布列及数学期望
．（附：回归方程
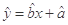中，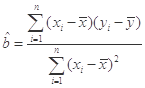
，
）
在平面直角坐标系
中，点
与点
关于原点
对称，
是动点，且直线
与
的斜率之积等于
．
（1）求动点的轨迹方程；
（2）设直线和分别与直线
交于点
，问：是否存在点使得
与
的面积相等？若存在，求出点的坐标；若不存在，说明理由．
设函数
，其中
．
（1）当
时，证明不等式
；
（2）设
的最小值为
，证明
．
选修4—1：几何证明选讲
如图，
内接于圆
，
平分
交圆于点
，过点
作圆的切线交直线于点
．
（1）求证：
；
（2）求证：
．
选修4—4：极坐标与参数方程
已知曲线
的参数方程是
（
为参数），以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程是
．
（1）写出的极坐标方程和的直角坐标方程；
（2）已知点
、
的极坐标分别为
和
，直线
与曲线相交于
两点，射线
与曲线相交于点
，射线
与曲线相交于点
，求
的值．
选修4—5：不等式选讲
设函数
．
（1）当
时，解不等式
；
（2）若
的解集为
，
，求证：
．