已知全集
，
，则
等于
A． |
B． |
C． |
D． |
设
，则“
”是“
”的（ ）
| A．充分而不必要条件 |
| B．必要而不充分条件 |
| C．充要条件 |
| D．既不充分又不必要条件 |
函数
的零点所在的区间为（ ）
A． |
B． |
C． |
D． |
设等比数列
的前项和为
，若
，则
= （ ）
A． |
B．  |
C．  |
D． |
定义在R上的函数
满足
，当
时，
，当
时，
．则
（ ）
A． |
B． |
C． |
D． |
已知函数
在区间
上是增函数,则常数
的取值范围是 （ ）
A． |
B． |
C． |
D． |
已知函数
，则不等式
的解集为（ ）
A． |
B． |
C． |
D． |
已知函数
的最小正周期是
，若其图像向右平移
个单位后得到的函数为奇函数，则函数
的图像 （ ）
A．关于点 对称 |
B．关于直线 对称 |
C．关于点 对称 |
D．关于直线 对称 |
已知函数
的图象在点
处的切线斜率为
，数列
的前
项和为
，则
的值为（ ）
A． |
B． |
C． |
D． |
下列四个图中，函数
的图象可能是（ ）
一个四棱锥的侧棱长都相等,底面是正方形,其正（主）视图如右图所示该四棱锥侧面积和体积分别是（ ）
A． |
B． |
C． |
D． |
已知定义域为
的奇函数
的导函数为
，当
时，
，若
，
，
，则
的大小关系正确的是（ ）
A． |
B． |
C． |
D． |
设
满足约束条件
，若目标函数
的最大值为
，则
的最小值为________________．
在三棱锥
中,
平面
，
，
，
,则此三棱锥外接球的体积为 ．
函数
对于
，总有
成立，则
= ．
在
中，
为的重心（三角形中三边上中线的交点叫重心），且
．若
，则
的最小值是________．
已知函数
．
（1）求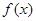
的最大值，并求出此时
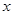的值；
（2）写出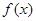的单调区间．
已知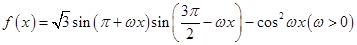
的最小正周期为
．
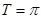（1）求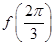
的值；
（2）在
中，角
所对应的边分别为
，若有
，则求角
的大小以及
的取值范围．
数列{
}的前
项和为
，是和
的等差中项，等差数列{
}满足
，
．
（1）求数列
，
的通项公式；
（2）若
，求数列
的前项和
．
如图，在四棱锥
中，
平面
，底面是菱形，
，
,
为
与
的交点，
为棱
上一点．
（Ⅰ）证明：平面
⊥平面
；
（Ⅱ）若
平面,求三棱锥
的体积．
已知函数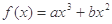
的图象经过点
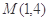，曲线在点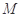
处的切线恰好与直线
垂直．
（1）求实数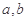
的值；
（2）若函数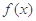
在区间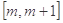
上单调递增，求
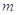的取值范围．
已知单调递增的等比数列
满足：
,且
是
,
的等差中项．
（1）求数列的通项公式；
（2）若
,
,求
．