如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. |
B. |
C. |
D. |
如图,在Rt△ABC中,tanB= ,BC=2
,BC=2 ,则AC等于( )
,则AC等于( )
| A.3 |
| B.4 |
C.4 |
| D.6 |
若△ABC在正方形网格纸中的位置如图所示,则tanα的值是( )
A. |
B. |
C. |
| D.1 |
在△ABC中,∠C=90°,AC=1,BC=2,则tanB是( )
A. |
B. |
| C.2 |
D. |
△ABC中,∠C=90°,tanA= ,∠B等于( )
,∠B等于( )
| A.30° |
| B.45° |
| C.60° |
| D.90° |
已知Rt△ABC中,∠C=90°,tanA= ,BC=8,则AC等于( )
,BC=8,则AC等于( )
| A.6 |
B. |
| C.10 |
| D.12 |
0.0010+(﹣ )﹣2﹣tan45°= .
)﹣2﹣tan45°= .
若a=3﹣tan60°,则 ÷
÷ = .
= .
如图,在梯形ABCD中,AD∥BC,AB=DC,AC⊥BD于点O,过点A作AE⊥BC于点E,若BC=2AD=8,则tan∠ABE= .
在Rt△ABC中,∠C=90°,AC=5,BC=4,则tanA= .
计算:tan45°+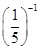 = .
= .
已知∠A为锐角,tanA=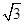 ,则∠A的余角是 .
,则∠A的余角是 .
如图,已知tanα=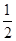 ,如果F(4,y)是射线OA上的点,那么F点的坐标是 .
,如果F(4,y)是射线OA上的点,那么F点的坐标是 .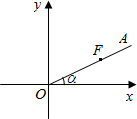
在正方形网格中,∠AOB的位置如图所示,则tan∠AOB的值为 .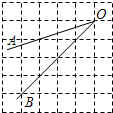
计算|2﹣tan60°|+2﹣2+ = .
= .
如图,三角形在方格纸中的位置如图所示,则tanα的值等于 .
﹣22+(tan60°﹣1)× +(﹣
+(﹣ )﹣2+(﹣π)0﹣|2﹣
)﹣2+(﹣π)0﹣|2﹣ |= .
|= .
计算:|﹣5|= ;﹣2﹣2= ;tan30°= .
已知长方形ABCD,AB=3,BC=1,则tan∠DAC= .
如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB= .
若 ,则
,则 = ;若∠A是等腰直角三角形的锐角,则tanA= .
= ;若∠A是等腰直角三角形的锐角,则tanA= .
∠A和∠B是一直角三角形的两锐角,则tan = .
= .
计算:|﹣1|+ ﹣tan45°= .
﹣tan45°= .
若△ABC中,∠C=90°,则 是∠A的 函数.
是∠A的 函数.
( tan70°)2009•(3tan20°)2009= .
tan70°)2009•(3tan20°)2009= .
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
计算 .
.
(1)计算: .(2)解方程
.(2)解方程 =0.
=0.
计算: .
.
计算: .
.