已知复数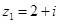
，
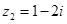，若
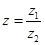，则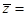
（ ）
A． |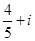
B． |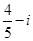
C． |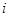
D． |
抛物线
的焦点坐标为
A． |
B． |
C． |
D． |
曲线
在点
处的切线方程为（ ）
A． |
B． |
C． |
D． |
【改编】命题“
为假”是命题“
为真”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
下列正确的是（ ）
| A．类比推理是由特殊到一般的推理 |
| B．演绎推理是由特殊到一般的推理 |
| C．归纳推理是由个别到一般的推理 |
| D．合情推理可以作为证明的步骤 |
已知命题
，命题
，则命题
是命题
成立的 （ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
【改编】一条直线经过抛物线
的焦点，且与
交于
、
两点．若
，则这条直线的斜率为 （ ）
A． |
B． |
C． |
D． |
【改编】已知
，
是
的导函数，即
，
，…，
，
，则
A． |
B． |
C． |
D． |
通过随机询问110名大学生是否爱好某项运动，得到如下的列联表：
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由上表算得k≈7．8，因此得到的正确结论是（ ）
| P（k2>k） |
0．50 |
0．40 |
0．25 |
0．15 |
0．10 |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
| k |
0．455 |
0．708 |
1．323 |
2．072 |
2．706 |
3．84 |
5．024 |
6．635 |
7．879 |
10．83 |
A．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”
B．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”
C．有99%以上的把握认为“爱好该项运动与性别有关”
D．有99%以上的把握认为“爱好该项运动与性别无关”
用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（ ）．
| A．假设三内角都不大于60度 |
| B．假设三内角都大于60度 |
| C．假设三内角至多有一个大于60度 |
| D．假设三内角至多有两个大于60度 |
阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为 （ ）
| A．7 | B．9 | C．10 | D．11 |
【改编】命题“若
，则
且
”及它的逆命题、否命题、逆否命题为真命题的个数为 ；
观察下列式子：
，
，
，
，
，由以上可推测出一个一般性结论：对于
，
的和
．
若函数
在区间
上为增函数，则实数
的取值范围是
已知抛物线
的焦点
和点
，
为抛物线上一点，则
的最小值是______________
【改编】在△ABC中，a，b，c为角A，B，C所对的边长，z1＝
，z2＝cos A＋
．若复数
为实数，试判断△ABC的形状．
【原创】设函数
（1）若
为函数
的极值点，求
的值
（2）在（1）的条件下，函数的图象的对称中心为
，求
的值;
设数列
的前
项和为
，且满足
．
（1）求
，
，
，
的值并写出其通项公式；
（2）用三段论证明数列是等比数列．
已知椭圆
的两个焦点为
，离心率为
，直线l与椭圆相交于A、B两点，且满足
O为坐标原点．
（1）求椭圆的方程;
（2）求
的最值．